В чем измеряется углы. В чем измеряется углы

Можно сказать, что одна сторона развернутого угла является продолжением другой стороны этого угла. На этой диаграмме показан расширенный угол C. Его значение составляет 180 градусов (180 0).

Измерение углов

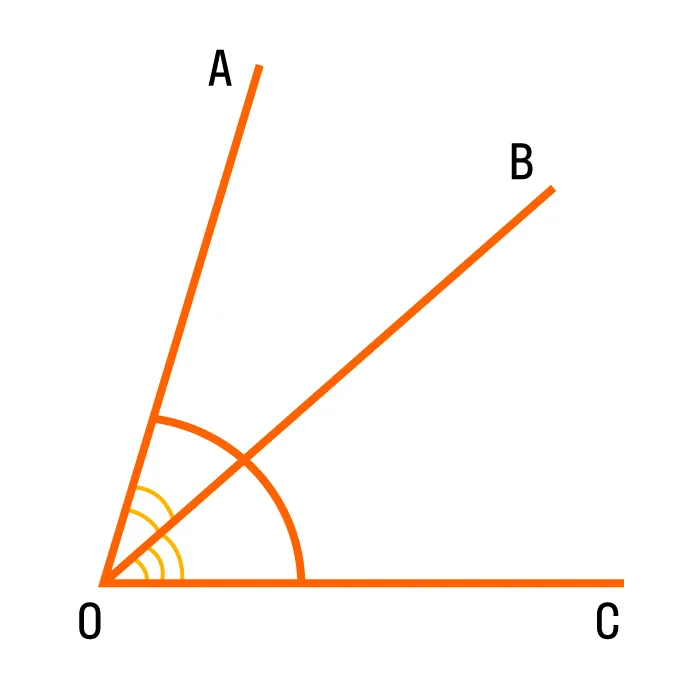
Когда линии пересекаются, существуют четыре различные области относительно точки пересечения. Эти новые области называются углами.

Показаны четыре различные области, образованные пересечением AB и CD.

Обычно углы измеряются в градусах, что обозначается как °. Когда объект совершает полный круг, то есть движется из точки D через B, C, A, а затем обратно к D, то говорят что он повернулся на 360 градусов (360°). Таким образом, градус — это $\frac$ круга.

Углы больше 360 градусов

При этом, когда объект проводит полный круг вокруг точки, он образует 360°, но когда он делает несколько кругов, он образует угол больше 360°. Это обычное явление в повседневной жизни. При движении автомобиля, т.е. колеса, оно образует угол больше 360°.

Чтобы найти количество окружностей (проходящих кругов) при вращении объекта, подсчитайте, сколько раз ему нужно прибавить к себе 360, чтобы получить число меньше заданного угла. Аналогично, умножьте число на 360, чтобы получить число, которое мало, но близко к определенному углу.

Пример 21.Найдите число циклов, описываемых объектом, образующим угол a) 380° b) 770° c) 1000°Решение. (a) 380 = (1 × 360) + 20 объектов описывают окружность, пройдя 20° $ 20 ^ = \ frac = \ frac $thecircle объект описал окружность 400 ⌘ frac$.

(b) 2×360 = 720 770 = (2×360) + 502 окружности и 50° $ 50 ^ = \ frac = \ frac$ окружности описывают объект 3,500° frac $ окружности c) 2×360 = 720 1000 = (2×360) + 280 $ 280 ^ = \ frac = \ frac$круги, описанные в пункте 3.500\frac$циклы

Положительные и отрицательные углы

При вращении объекта по часовой стрелке он образует отрицательный угол поворота, а при вращении против часовой стрелки — положительный угол поворота. До сих пор рассматривались только положительные углы.

В форме диаграммы отрицательный угол может быть изображен так, как это показано ниже.
Рисунок ниже показывает знак угла, который измеряется от общей прямой, 0 оси (оси абсцисс — х оси)

Это означает, что любой отрицательный угол может иметь соответствующий положительный угол. Например, нижняя часть вертикальной линии равна 270°. Измеренное в отрицательном направлении, оно равно -90°. Просто вычтите 270 из 360. Если угол отрицательный, прибавьте 360, чтобы получить соответствующий положительный угол. Если угол равен -360°, это означает, что объект рисует несколько кругов по часовой стрелке.

Пример 31. Найдите соответствующий положительный угол a) -35°b) -60°c) -180°d) -670°

2. найдите соответствующие отрицательные углы 80°, 167°, 330° и 1300°.Решение. 1. прибавьте 360 к значению угла, чтобы найти соответствующий положительный угол. (a) -35° = 360 + (-35) = 360-35 = 325°b) -60° = 360 + (-60) = 360-60 = 300°c) -180° = 360 + (-180) = 360-180 = 180°d) -670° = 360 + (-670) = -310 Это означает, что по часовой стрелке (360) 360 + (- 310) = 50°. Угол равен 360 + 50 = 410°.

2. чтобы получить соответствующий отрицательный угол, вычтите 360 из значения угла. 80°=80-360=-280°167°=167-360=-193°330°=330-360=-30°1300°=1300-360= 940 (круг 1) 940-360 = 580 (круг 2) 580-360 = 220 (круг 3) 220-360=-140°Угол равен 360-360-360-140 = -1220°, поэтому 1300° = -1220°.

Измерить угол — значит найти его величину. Углы делятся на три типа: острые, тупые и прямые. Прямой угол равен 90°. Угол больше 90° — тупой угол, а угол меньше 90° — острый угол. Вытянутый угол равен 180 градусам.

Угловые призматические меры и угольники

Измерения угловой призмы используются для хранения и транспортировки плоских угловых единиц. Они используются для контроля специфики и угловых размеров различных изделий. Для градиентного уклона и прямых измерений. Угол, используемый для проверки угловых и рабочих измерений, называется опорным углом.

Углы делятся на четыре категории (1, 2, 3 и 4), в зависимости от точности аккредитации. Угловые измерения первой категории имеют предельную погрешность ± 0,5″, второй категории — 1″, третьей категории — 3″ и четвертой категории — 6″. Угловые измерения собираются в блоки с помощью специальных рецепторов.

Углы контролируются путем оценки зазора между углом и деталью, который контролируется на глаз или путем сравнения с эталонным зазором, созданным с помощью наличника и линейки. При больших углах освещения люмены оцениваются с помощью змеек. Погрешность при контроле углов зависит от погрешности самого угломера, длины контролируемого угла и других факторов.

Угломеры с нониусами

Счетчик углов Нониуса используется для измерения углового профиля детали с помощью детектора углов Нониуса точно 2′ и 5′. Он состоит из кругового диска для измерения угла, закрепленного на корпусе с помощью затянутой гайки. На основании имеется регулировочная лента и верриеро, по обе стороны от точки отсчета отмечено 30 классов. Каждая оценка соответствует двум минутам. Harakas имеет продольный скользящий часовой механизм спереди, вдоль которого перемещается зажимное напряжение, когда линейка находится в углу.

Корнеометр размещают на контролируемом уровне так, чтобы линейка и поверхность тела были совмещены для измерения со сторонами угла. Целое число измеряется по шкале диска на нулевом градиенте (линии) Луны. Затем определите месячный градиент, совпадающий с делением основной шкалы (диска). Затем, используя нониус, найдите минуты и градусы, которые совпадают с делениями нониуса.

Оптический угломер

Оптические телескопы оснащены стеклянным диском. На стеклянном диске указаны градусы и минуты. Цена за постепенный уклон составляет 10 ‘. Основная (фиксированная) линейка строго закреплена на корпусе. На диске установлены лупа, рычаг и раздвижная линейка. Под лупой вместе со стеклянным лотком находится небольшая стеклянная пластина, на которой нанесены индикаторы, хорошо видимые через окуляр. Линейки перемещаются вместе и могут быть стабилизированы в нужном положении с помощью рычага.

Когда линейка вращается в одну сторону, диск и увеличительная линза вращаются в том же направлении. Таким образом, определенная линейка на линейке соответствует определенному положению диска и увеличительной линзы. После затягивания грации с помощью затяжного кольца угломер считывается через увеличительную линзу. С помощью визуального ангиометра можно измерять углы от 0° до 180°. Допустимая погрешность визуального отображения ярости составляет ± 5 ‘.

В математике углы измеряются в направлении оси абсцисс (то есть по отношению к направлению вправо от первого наблюдателя) и отсчитываются влево.

Углы образованные при пересечении двух прямых

Когда две линии пересекаются, образуются два разных угла.

Смежные углы

Два угла называются смежными, если они имеют общую вершину и одну общую сторону, а две другие стороны лежат на одной прямой и образуют развивающийся угол. Смежные углы дополняют друг друга, потому что они являются продолжением друг друга.

隣接するコーナーのプロパティ

1. 隣接する角の合計は180°です。
2. 両方の隣接する角は互いに等しくなりますが、それらは正しい角度です。
3. В паре смежных углов один угол всегда острый, а другой — тупой, или оба угла прямые.
4. 半分のコーナーは平等です。
5. Косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположные знаки.

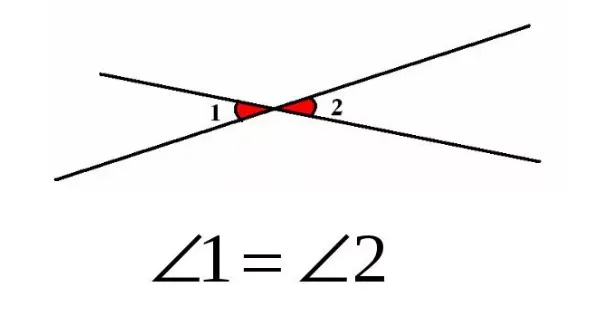
Вертикальные углы

Перпендикулярные углы — это пара углов, в которой стороны одного угла являются продолжением сторон другого угла.

プロパティ：垂直角度は等しい。

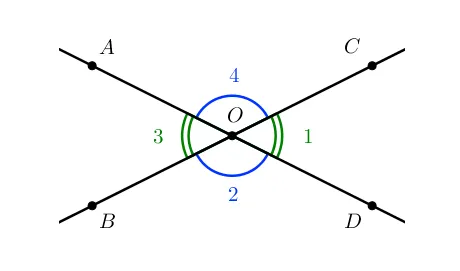
カップル1および3、2、4は垂直です。

垂直角度の容量で：：

コーナーのペア1と2、2、3、3、4、4、4、4、および1は隣接しています。

隣接する角度の能力：

\ угол c o d+\ угол d o b = 180^\\\\\\\

\\\\\ {\\\\\\\ угол d o b+\ угол b o a = 180^\

\\\\\\ {\ угол b o a+\ угол a o c = 180^\\\\\\\\

\ угол a o c+\ угол c o d = 180^\。

隣接する角度	コーナー
共通の側面と上部を持つ2つのコーナーは、隣接する角度と呼ばれます。	Когда две прямые пересекаются, пары противоположных углов, образованных в вершине, называются перпендикулярными углами.
共通の側面と共通のトップを持っています。	共通のトップを持っていますが、共通の側面はありません
隣接するコーナーのサイズは必ずしも等しいとは限りません	垂直反対の角度のサイズは等しい。

Разница между смежными и вертикальными углами

Сравнение углов

Самый простой метод, метод суперпозиции, может быть использован для сравнения углов. Он предполагает выравнивание двух вершин и стороны одного угла со стороной другого. これらの角度の側面が一致する場合、角度は等しくなります。それ以外の場合、もう一方にある角度は小さくなります。等しい角度と不平等な角度の2つの例を次に示します。

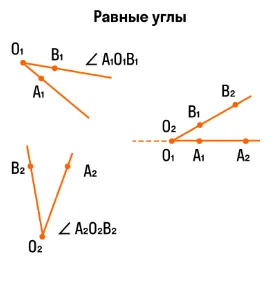
Поэтому \угольник A_ O_ B_\ и \угольник A_ O_ B_\ идеально конгруэнтны при наложении: \угольник A_ O_ B_=\угольник A_ O_ B_\

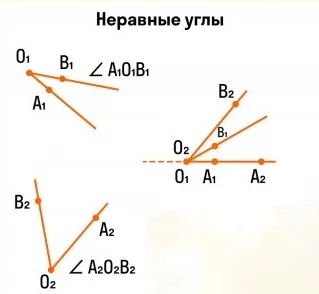
Угол A_ O_ B_\ и угол A_ O_ B_\ не пересекаются: \угол A_ O_ B_

eq \угол A_ O_ B_\

したがって、ラッピングのない角度は常に等しくなります。

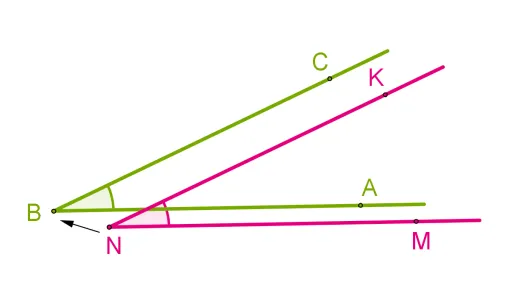
1. 角度\角度a b c \ и \ угол m n k \は次のように整列しています。
2. 一方のコーナーの上部Bをもう一方のコーナーの上部Nに合わせます。

Сторона BA одного угла пересекается со стороной NM другого угла, так что стороны BC и NK лежат в одном направлении.

Если нет, то один угол — меньше другого: ∠ABC

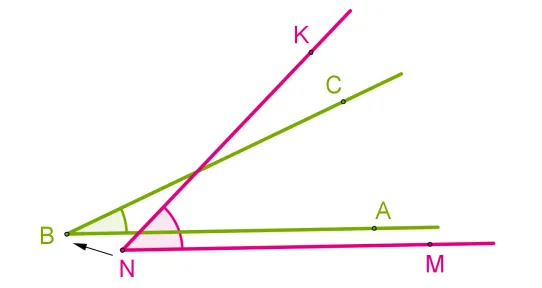
反対側が一致する場合、角度は等しくなります：∠ABC=∠MNK。

1. 線と角度に基づいたいくつかの重要な定理：
2. Если две параллельные прямые пересекаются вторичной прямой, то смежные внутренние углы имеют одинаковое значение.
3. Если две параллельные прямые пересекаются по малому углу, то противоположные внешние углы имеют равные величины.
4. Если две параллельные прямые пересекаются вторичной прямой, то их соответствующие углы имеют равные величины.
5. Если две параллельные прямые пересекаются вторичной прямой, то внутренние углы являются касательными к одной и той же стороне этой вторичной прямой.

Измерение углов

垂直角は、線が直線的に交差すると等しくなります。線は、平行または非平行である場合があります。

Градусная мера

いくつかの角度の測定単位があります。。最も一般的に使用される測定単位を見てみましょう。

Полный оборот, то есть когда начальная и конечная стороны находятся в одном положении после вращения по часовой или против часовой стрелки, делится на 360 единиц, называемых градусами. Таким образом, если поворот от исходной стороны к конечной стороне составляет \left(\facing right)\ one turn, то угол, как говорят, имеет меру в один градус. Он обозначается как 1°.

Радианная мера

Мы измеряем время в часах, минутах и секундах, где 1 час = 60 минут и 1 минута = 60 секунд. Аналогично, при измерении углов

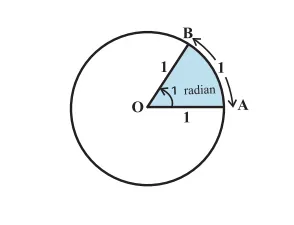
Радиальные измерения немного сложнее, чем измерения уклона. Представьте себе круг с радиусом в одну единицу. Затем представьте дугу длиной в одну единицу. Угол, образующий эту дугу в центре окружности, имеет радиальную меру. Внешний вид:.

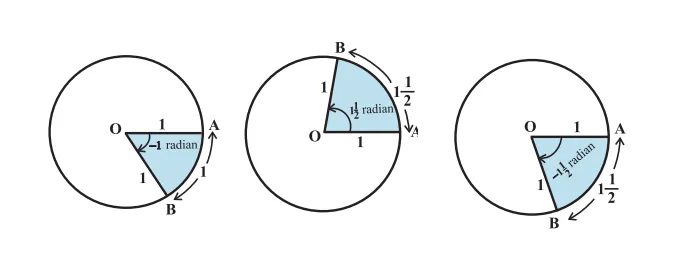
Вот другие примеры углов: -1 радиан, радиан, Lo_ 1 \ frac \ радиан, Lo_ -1 \ frac \ радиан.

Длина окружности = \ 2 \ pi r \ ldots \ где r — радиус окружности. Таким образом, для окружности радиуса 1 единица периметра равна Lo_ 2 \ пи \ радиан Таким образом, полный поворот исходной стороны образует угол ʒ 2 \ pi pi \ radio в середине. Подведем итоги:.

Связь между степенью и радианными мерами

В Лейлине есть дуга с одним рядом радиусов в центральном углу. Таким образом, в окружности радиуса, лук длиной l лежит под углом = \ pi \ frac \ radios. Обобщая, можно сказать, что если дуга длиной l образует центральный угол радиуса, то это цикл Рэлея.

Из определения судьбы и радиуса мы знаем, что угол, образованный центральной окружностью, равен<\pi>Следовательно, ǫ 2 \ пи \ радиус = 360°⇒ ǫ пи \ радиус = 180°. Далее, заменим приблизительную цену Ј1 радиуса \ pi \ как \ frac \ на вышеприведенное уравнение: 1 радиус \ frac><\prime>= 57^ 16^<\pi>\᥉. Также, ᥉ 1^= \ frac

> \ радиус = 0,01746 радиуса. Ниже приведена таблица, показывающая связь между некоторыми распространенными угловыми градусами и лучами света.	Градусы	\ 30^\	\ 45^\	\ 60^\	\ 90^\	\180^\ \180^\	\ 360^\ \ 90^\ \ 90^\ \ 360^\ \ 360^\ \ 360^\
Всплеск	\ ГРП<\pi>\ \frac	\ ГРП<\pi>\ \frac	\ ГРП<\pi>\ \frac	\ ГРП<\pi>\ \frac	\ \ \ \ \ \ \ \	\ ГРП<3\pi>\ \frac	Переведите 40°20 ‘ в радиан.

Решение: 1° = 60′, следовательно, 20′ = \ \ \ pi \ frac> \.

Радиальная мера = \섹 frac.

> x \ градусная мера.<\pi>Следовательно, радиальная мера Lo_40^ 20^

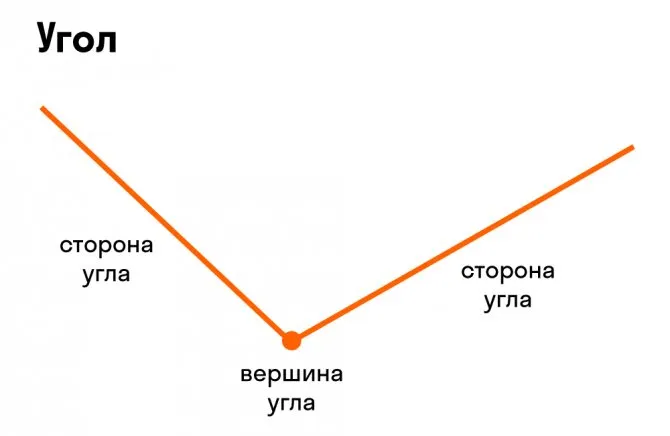
= \ frac<\prime> \ раз \ frac = \ frac \ радиан.<\pi>Все геометрические фигуры состоят из точек, линий, лучей и плоских поверхностей. Когда две прямые или лучи встречаются в какой-то момент времени, измерение между двумя линиями называется углом. В этой статье объясняется, что такое угол, различные типы углов и что означает пример.

Смежные углы — это два угла с общей вершиной, одна сторона которых общая, а другая лежит на одной прямой (не совпадает). Сумма смежных углов равна 180°.

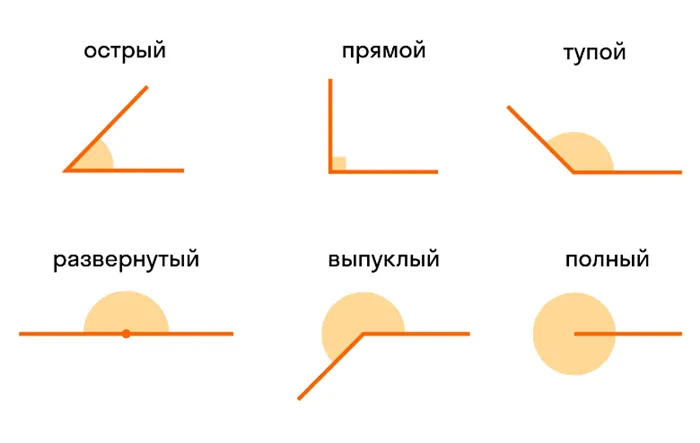
Типы углов

• Вертикальный угол — это два угла, образованные пересечением двух прямых линий, не имеющих общих сторон. Другими словами, два угла называются перпендикулярными, если сторона одного угла является продолжением стороны другого угла. Вертикальные углы равны.

• Центральный угол находится в верхнем углу в середине круга. Центральный угол равен градусу дуги, заключенной между сторонами угла.

• Зарегистрированный угол — это угол, вершина которого находится в окружности, а стороны пересекают окружность. Записанный угол — это половина лука, заключенного в его сторонах.

• Угол делится на углы в зависимости от размера.

Острый (0-90°) (90°)

• Тупой (от 90° до 180°)
• Косые (не равные 90° или 180°)
• Неизогнутый (180°)
• Неизогнутые (от 180° до 360°)
• Облик (360°)
• Угол между прямой и ) — это угол, на который прямая вращается против часовой стрелки. Углы, отличные от , считаются равными. Обратите внимание на направленные углы (агрегаты) между линиями. Угол направления имеет следующие характеристики: a); c) точка.

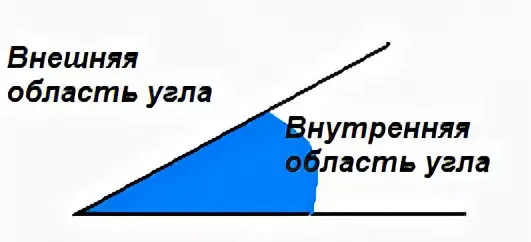
Вариации и обобщения

В некоторых практических задачах полезно думать об угле как о форме, получающейся в результате вращения фиксированного луча вокруг точки O (из которой начинается луч) в заданном положении. В этом случае угол является мерой поворота луча. Такое определение позволяет обобщить понятие угла: в зависимости от направления вращения различают положительные и отрицательные углы, рассматривают углы больше 360°, углы, равные 0°, и т.д. В тригонометрии это соображение позволяет исследовать тригонометрические функции для любых значений аргумента.

Понятие угла также обобщается на различные объекты, рассматриваемые в стереометрии (двугранный угол, многогранный угол, телесный угол).

Мы также рассмотрим угол между гладкими кривыми в точке контакта: по определению, он равен углу между касательными к кривым.

Одним из самых распространенных инструментов для построения и измерения углов является транспортир, который обычно используется для построения угла определенного размера. Для более точного измерения углов было разработано множество точных приборов:

Измерение углов

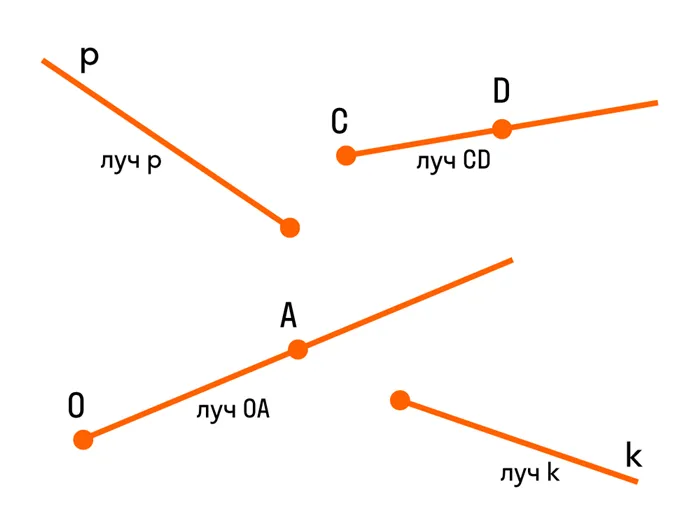
Можно сформулировать определение иначе: если из вершины любого угла провести луч и разделить угол на два, то образовавшиеся углы будут смежными.

— использовался в области судоходства, для определение положения судна в море или океане — применялся для измерения высоты Солнца над горизонтом с целью определения географических координат той местности, в которой производится измерение и на судах — один из первых инструментов для астрономических наблюдений, служащий для измерения углов.

意味。 Два угла являются смежными, если у них есть общая сторона и две другие стороны, которые являются падающими лучами.

Смежные углы. Вертикальные углы

Если на рисунке 70 OA и OB являются дополняющими лучами, то AOS и BOS являются смежными.

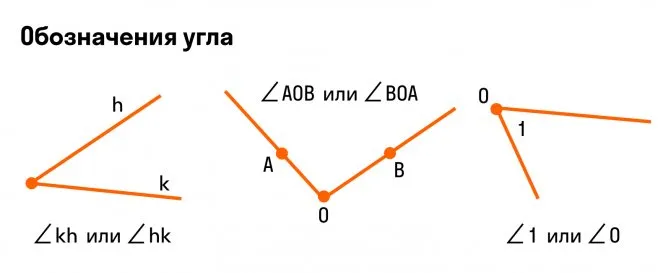
Теорема (свойство смежных углов).隣接する角の合計は180°です。

証拠：

Дано:
Доказать:

Если смежные углы равны, то каждый из них является прямым углом.

Из определения смежных углов следует, что лучи OA и ОВ являются дополнительными и поэтому образуют развернутый угол АОВ, равный 180°. Луч ОС проходит между сторонами этого угла, и по аксиоме измерения углов Поэтому

1. Если два угла равны, то их смежные углы также равны.
2. ノート。 Все теоремы в геометрии 7-9 классов описывают свойства фигур на плоскости.

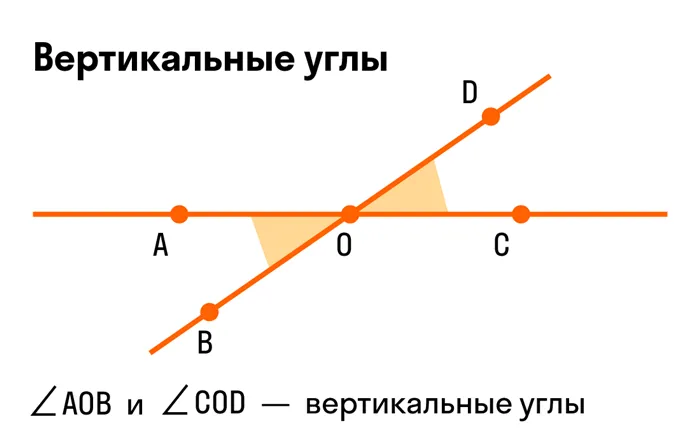
意味。 Два угла называются вертикальными, если стороны одного угла касательны к сторонам другого.

Пересечение прямых AC и DB в точке O (Рисунок 71) означает, что OA и OS, OB и OD являются дополнительными лучами. Поэтому углы AOD и BOC являются вертикальными. Углы AOB и DOC также являются вертикальными.

Теорема (свойство вертикальных углов). Вертикальные углы равны.

証拠：

Дано:

Доказать:

Если смежные углы равны, то каждый из них является прямым углом.

から

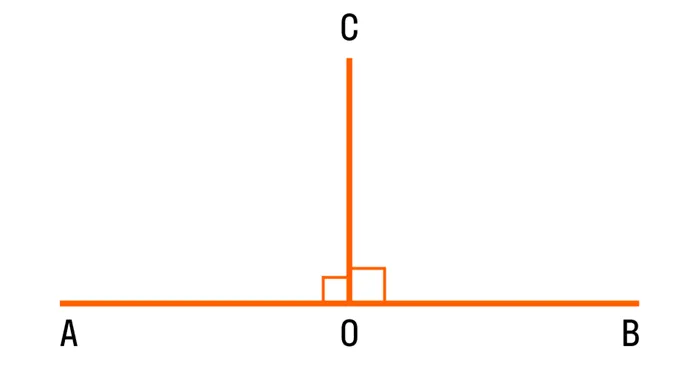
Пересечение двух прямых дает четыре угла (без учета открытых углов). Если один из них равен 90°, то остальные также равны 90° (докажите это сами). Считается, что прямые линии пересекаются под прямым углом.

Углом между двумя пересекающимися прямыми называется меньший из образованных ими углов. Если при пересечении прямых АВ и CD (рис. 73)

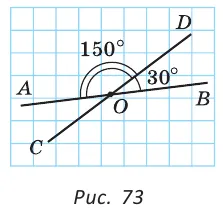
Считается, что угол между параллельными прямыми равен 0°.

Смежные углы относятся как 2:3. a) Найдите значение каждого из углов, b) Определите, какой процент от развернутого угла составляет меньший угол.

Пример №4

α) Пусть ). по свойству смежных углов.

Углы, плоскости и квадранты