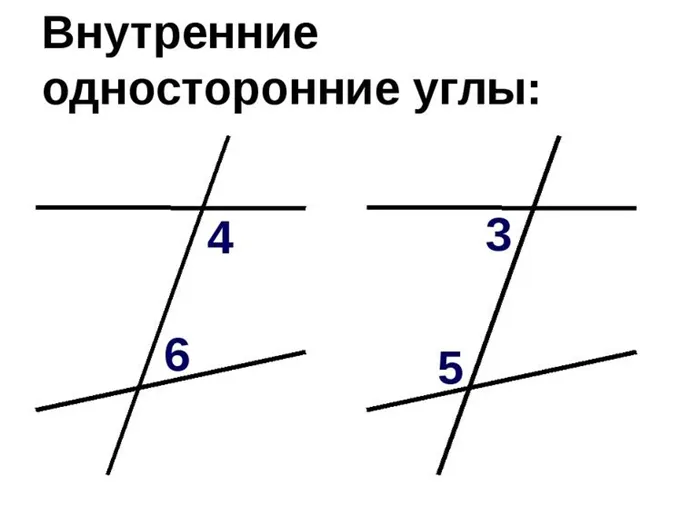
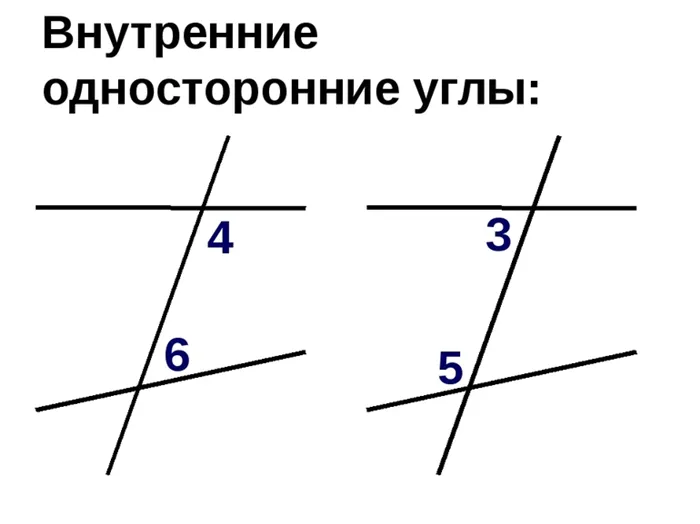
Что такое внутренние углы. Что такое внутренние углы

Другими словами, не все углы вне треугольника имеют право называться внешними, а только те, которые образуются при продолжении одной стороны и другой.

Что такое внутренние углы

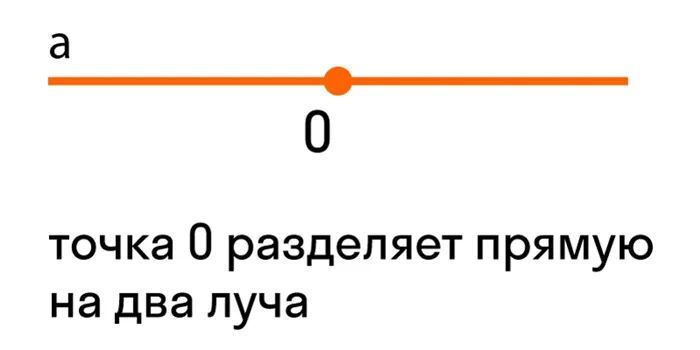
Угол — это геометрическая фигура, образованная двумя лучами, исходящими из одной точки.

Точка, из которой исходят лучи, образующие угол, называется вершиной угла. Лучи света, образующие угол, являются его гранями.

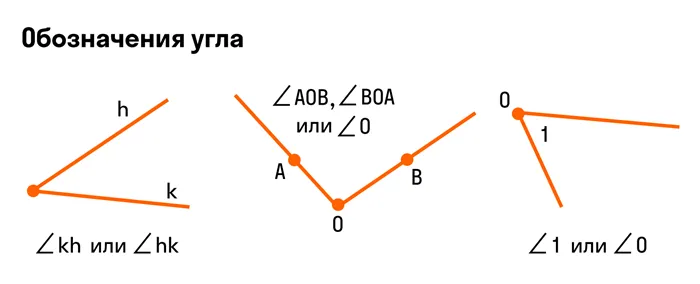
Угол может быть назван по имени его вершины или по имени образующих его лучей. Однако лучше всего называть угол, взяв вершину угла в качестве начальной точки обоих сегментов, а затем сегмент луча, образующего его, как в angle line.

．

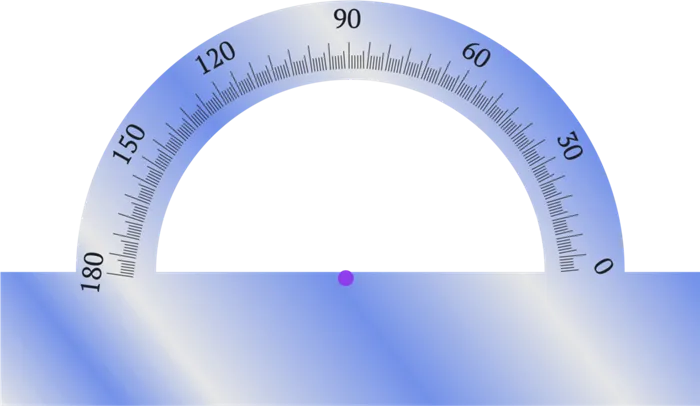
Градусная мера угла

Углы выражаются в градусах. Представьте, что первоначально два луча, образующие угол, были одинаковыми. Циферблат часов можно представить как минутную и часовую стрелки, наложенные друг на друга в полдень. С течением времени минутная стрелка все больше и больше удаляется от часовой, но они по-прежнему имеют общую точку, или ось.

Независимо от размера часов или длины стрелок, все часы показывают одно и то же время. Другими словами, стрелки часов с течением времени расходятся в одинаковой степени, хотя расстояние между двумя концами разное. В 3 часа дня угол между стрелками составляет 90 градусов, а в 6 часов вечера — 180 градусов. На основе этого значения вычисляются градусы остальных углов. Другими словами, угол между минутной и часовой стрелками составляет 60 градусов в 14:00 и 30 градусов в 13:00.

Угол в 180 градусов называется углом расширения.

Соединив точки пересечения биссектрис и параллелограмм ABCD, мы можем построить ABCD. Чтобы доказать, что полученная фигура является параллелограммом, рассмотрим следующее.

Типы углов

Существуют следующие типы углов, в зависимости от их числового значения (рис. 5)

• Нулевой угол (0°). Грани угла конгруэнтны. Его внутренняя область — пустое множество.
• Острые углы (больше 0°, но меньше 90°).
• Прямой угол (90°). Стороны прямого угла перпендикулярны друг другу.
• Тупой угол (больше 90° и меньше 180°).
• Невыпуклые углы (180°).
• Невыпуклые углы (в том числе от 0° до 180°).
• Выпуклые углы (больше 180°, но меньше 360°).
• Полярные углы (360°).

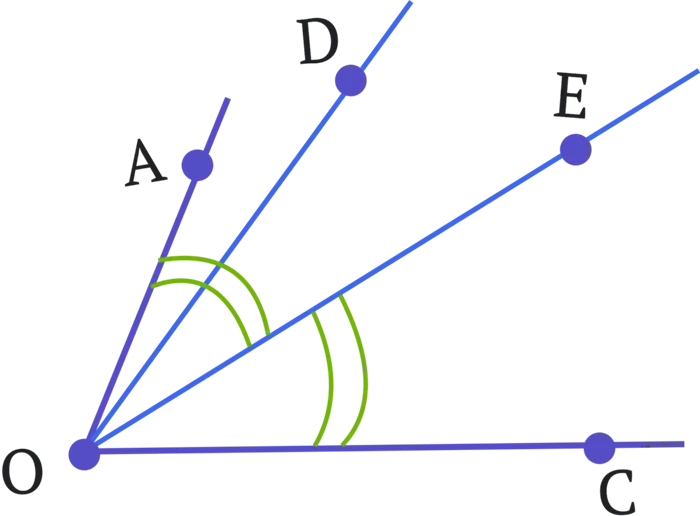
Сравнение углов

Углы можно сравнивать. То есть, можно определить, равны ли они, какие углы меньше, а какие больше. Чтобы выяснить, равны ли они, один угол нужно придвинуть к другому так, чтобы сторона одного угла прилегала к стороне другого угла, а две другие стороны были одинаковыми сторонами этого угла. Если две другие стороны также совпадают, то они конгруэнтны и, следовательно, равны. Если они не конгруэнтны, то меньшим считается тот угол, который является частью другого.

На рисунках 6a и 6b показаны два угла, 1 и 2. На рисунке 7 угол 2 меньше угла 1, потому что угол 2 является частью угла 1. Он написан следующим образом.

В случае с точкой A ₁ и А _{n +1} совпадают, то линия называется замкнутой полилинией (рис. 2) и разомкнутой полилинией (рис. 1), если они не совпадают.

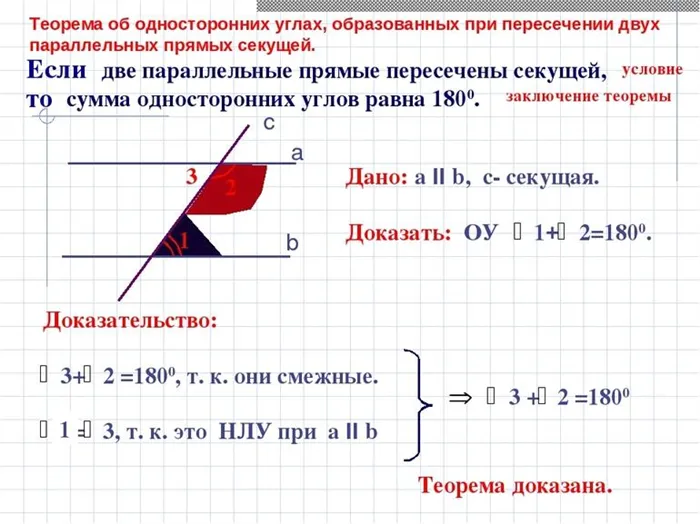
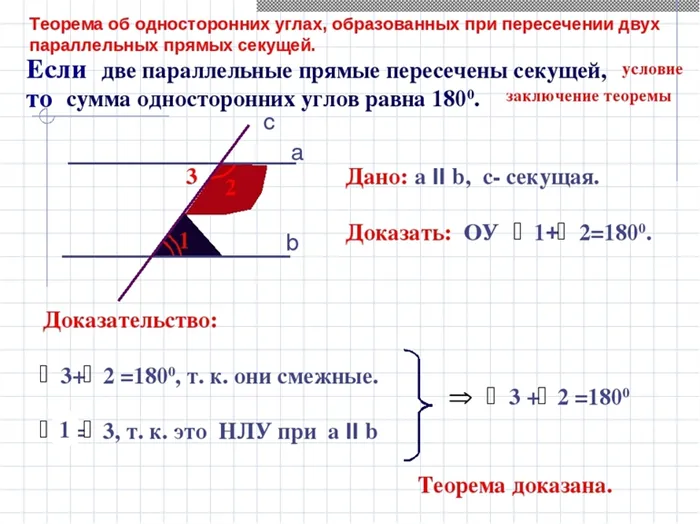
Доказательство теоремы

Прямая параллельна, если сумма внутренних углов одной стороны равна 180. Мы должны доказать теорему на основе исходных данных: секущая AB — это линия, на которой пересекаются параллельные прямые a и b.

Для доказательства теоремы можно предположить, что прямые пересекаются в некоторой точке C, так как они не параллельны. Это объясняется тем, что отрезки прямой AB образуют треугольник ABC с a и b, а C лежит в одной из двух плоскостей к AB. Линия a — сторона треугольника AC, а линия b — BC.

Если точку C1 построить на противоположной полуплоскости, то образуется треугольник ABC и другой треугольник ABC1; углы ABC и ABC1 равны. Как указано в постановке задачи, сумма ABC и CBA равна 180. Следовательно, сторона AC1 принадлежит a. Аналогично, BC1 принадлежит линии b.

Точка пересечения C прямых a и b принадлежит этим прямым. Однако С1 не принадлежит ни к той, ни к другой линии. Это связано с тем, что C1 лежит на полуплоскости и, по построению, линии не пересекаются.

Если сумма односторонних углов равна 180, то ABC1 не существует, поэтому a | b.

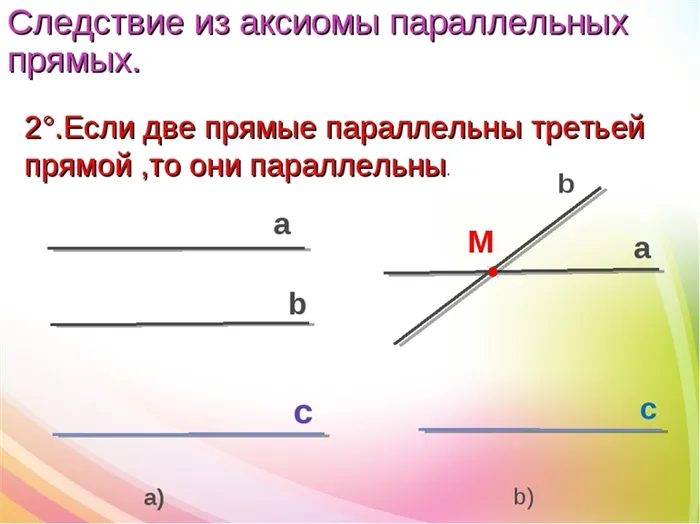
Следствие из свойства прямых

На прямую a из любой точки A, не принадлежащей данной прямой, можно опустить один перпендикуляр. Доказательство этого утверждения основано на следующей процедуре.

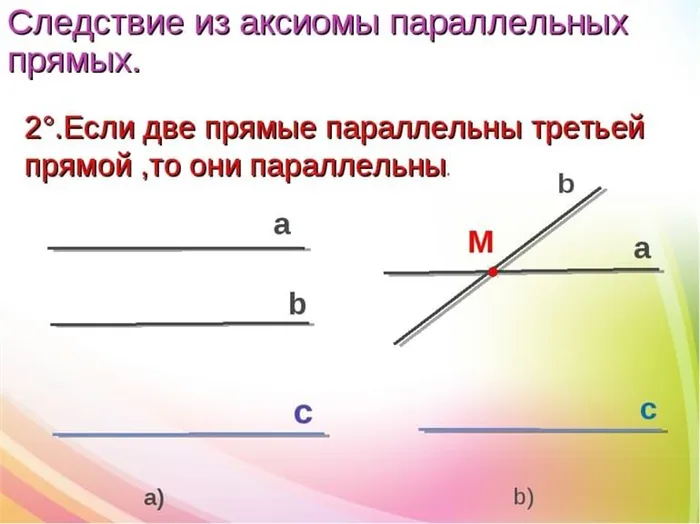
То есть, прямая AB — единственная вертикальная прямая, проходящая через точку A.

Сумма длин любых двух сторон треугольника больше длин трех его сторон, т.е. \ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ.

Равенство треугольников

Теперь, что если треугольников больше одного? Как проверить, равны ли они? Вообще-то, по определению.

Два треугольника равны, если они конгруэнтны при наложении.

Но… Это очень неудобное определение! Как можно наложить два треугольника даже в блокноте!

Но, к счастью, существуют знаки равных треугольников, которые позволяют действовать обдуманно, не рискуя своей записной книжкой.

Также, отбросив глупые шутки, я открою вам секрет. Для математиков «складывать треугольники» означает не разрезать и складывать треугольники, а говорить много-много-много слов, доказывающих, что два треугольника конгруэнтны при складывании.

Это происходит потому, что никто не может гарантировать отсутствие ошибки при их наложении с погрешностью, скажем, в четверть миллиметра.

Итак, некоторые математики сказали много-много слов, но мы не будем их повторять (разве что на последнем уровне теории) и будем активно использовать три равенства треугольника.

Первый признак равенства треугольников

Если две стороны одного треугольника и угол между ними равны двум сторонам другого треугольника и углу между ними, то можно сказать, что эти треугольники равны.

Второй признак равенства треугольников

Если одна сторона и два смежных угла одного треугольника равны одной стороне и двум смежным углам другого треугольника, то они равны.

Третий признак равенства треугольников

Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

В общем (математическом) представлении принято такое сокращение, которое легко запомнить и применять.

1. Первый знак обусловлен наличием двух сторон и угла между ними.
2. Второй — по двум углам и смежным сторонам.
3. Третий — с трех сторон.

Бонусы: Вебинары из нашего курса по подготовке к ЕГЭ по математике

В этом разделе вы найдете несколько вебинаров по курсам подготовки к ЕГЭ по математике.

16 сложных заданий ЕГЭ на доказательство подобия треугольников, до самых простых (но важных!) на площадь фигуры на листе шашечной бумаги. от (максимальный балл получает менее 1% студентов!) ,.

Выберите вебинар в соответствии с вашими сильными сторонами и развивайте свои навыки решения проблем!

ЕГЭ 3. Площадь фигур на клетчатой бумаге

Флокированная бумага очень полезна для геометрии. Причина этого в том, что очень легко нарисовать прямые углы.

А если к отрезку прямой добавить прямой угол, то получится прямоугольный треугольник. В случае прямоугольных треугольников, если вы запишите теорему Пифагора, длина отрезка уже определена, не так ли?

Хотя задача по геометрии с клетчатой бумагой не включена в ЕГЭ в 2021 году, это очень полезная задача для начала изучения геометрии и понимания планиметрии.

ЕГЭ 6. Прямоугольный треугольник: свойства, теорема Пифагора, тригонометрия

Большинство задач планиметрии решаются с помощью правильных треугольников.

Почему это так? Потому что не во всех задачах речь идет о треугольниках вообще, не говоря уже о прямоугольниках. Однако этот урок подтвердит, что это действительно так.

Редко какая проблема решается одной теоремой, в большинстве случаев она разбивается на несколько более мелких проблем. И в конце концов, мы имеем дело с треугольниками, причем прямоугольными.

В этом видео вы узнаете, как решать задачи на правильный треугольник из ЕГЭ, изучите необходимые теоремы и затронете основы тригонометрии.

ЕГЭ 6. Равнобедренный треугольник, произвольный треугольник

В этом видео вы узнаете все свойства равнобедренных треугольников и научитесь применять их для решения задач ЕГЭ.

Очень часто в равнобедренных треугольниках все «проблемы» решаются путем создания высот.

Вы также узнаете, как решать «обычные» треугольники. Проверьте правильность того, что мы говорили в предыдущем уроке о правильных треугольниках https://youtu.be/ZKGTVfaiGe8) — очень часто решение задач сводится к нескольким правильным треугольникам.

ЕГЭ 6, 14, 16. Теорема косинусов и синусов

Универсальными инструментами для решения треугольников являются теоремы косинусов и синусов. Они подходят для всех треугольников, а не только правильных (например, теорема Пифагора).

И как вы уже знаете, большинство проблем в планиметрии можно отнести к треугольникам.

В этом уроке вы изучите теорему и примените ее для решения первой части задачи.

ЕГЭ 16. Подобие треугольников. Задачи на доказательство

Это одна из самых сложных задач ЕГЭ по профильному предмету: менее 1% учащихся набирают идеальный балл 3!

Основная трудность заключается в построении доказательства. Баллы снимаются, если в шагах доказательства есть пропуски.

Например, часто считается само собой разумеющимся, что треугольники на рисунке похожи, и студенты забывают указать доказательства этого. За это снимаются баллы.

В этом видео вы узнаете, как применять подобие треугольников в доказательствах и как доказывать каждое умозаключение, указывая знак подобия.

Вы узнаете, как правильно записывать решение задачи и как сокращать свои записи, чтобы не тратить время на запись всех своих идей и полного названия теоремы.

Точка пересечения C прямых a и b принадлежит этим прямым. Однако С1 не принадлежит ни к той, ни к другой линии. Это связано с тем, что C1 лежит на полуплоскости и, по построению, линии не пересекаются.

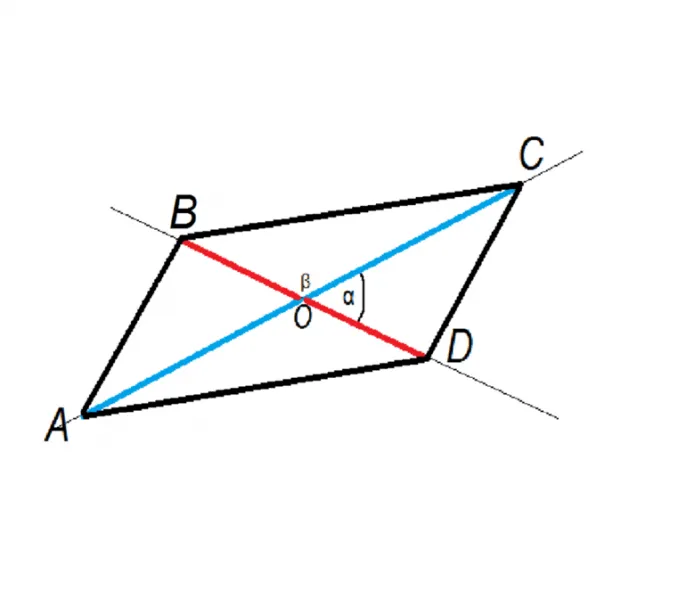
Построение параллелограмма

Если углы с одной стороны не прямые, то один из них острый, а другой тупой, т.е. меньше или больше. Если через каждую из них провести биссектрису, то она должна пересечь противоположную сторону в какой-то точке. Для этого мы можем с помощью компаса провести отрезок прямой на параллельной прямой, равной AB.

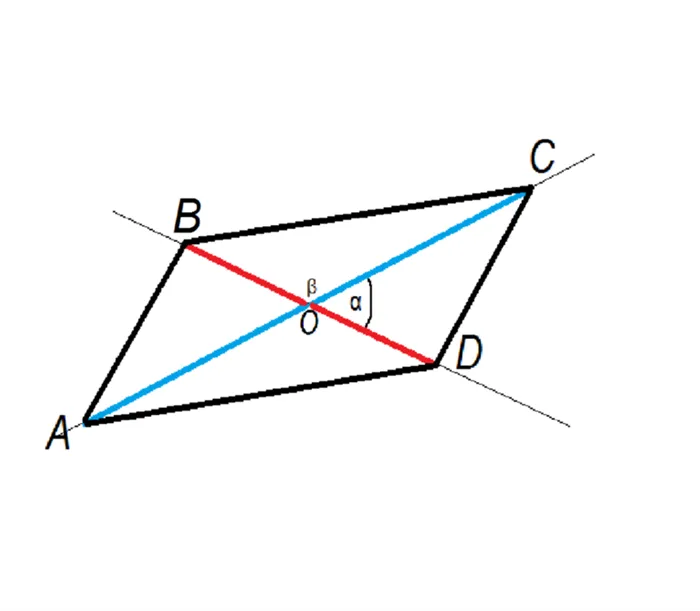
Отрезки, принадлежащие биссектрисе, вместе с параллелями образуют два треугольника. Противоположная сторона большего угла является биссектрисой, которая рассекает наибольший отрезок. Теорема о соотношении между углами и сторонами неравностороннего треугольника подтверждает это.

Соединив точки пересечения биссектрис и параллелограмм ABCD, мы можем построить ABCD. Чтобы доказать, что полученная фигура является параллелограммом, рассмотрим следующее.

1. По построению, AB=BD=AD.
2. Следовательно, AB=CD.
3. Точки C и D равноудалены от A и B.
4. Отрезки прямых AB и CD параллельны.
5. Получившаяся фигура ABCD является параллелограммом, так как стороны параллельны друг другу.

Построение равноудаленных точек C и D от A и B дает отрезок прямой CD, параллельный AB. Тогда CD — это отрезок прямой, перпендикулярный параллелям BC и AD. Поскольку все прямые отрезки полученной фигуры ABCD пересекаются перпендикулярно, она является прямоугольником по построению.

Доказательство теоремы позволяет определить, каково значение второго из двух внутренних углов в параллельной и делимой прямой. Решая геометрические задачи, можно определить их степени, которые зависят от разности.

Это происходит потому, что никто не может гарантировать отсутствие ошибки при их наложении с погрешностью, скажем, в четверть миллиметра.

Определение 5. Два угла называются смежными, если они имеют общую сторону и их сумма равна 180° (рис. 1).

Определение 6. Внешний угол многоугольника — это угол, прилежащий к внутреннему углу многоугольника (рис. 2).

Свойства углов треугольника

Сумма углов треугольника равна 180°.

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним

Углы треугольника.

Сумма углов треугольника равна 180°.

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним