Построение развертки конуса. Как рассчитать конус под определенный диаметр

Постройте наборы цилиндрических каналов. Навык 1: Соберите металлическую конструкцию. Навык 2: Конструирование наборов цилиндрических воздуховодов. Навык 3: Строительство конусов и воронки. Наблюдение за горячей формовкой не превышает предельную температуру молекулярной структуры материала.

Как сделать конус из листа металла. Развертка конуса

Иногда задача состоит в том, чтобы построить защитный зонт для вытяжной трубы или дымохода, вытяжную перегородку для вентиляционной системы и т.д. Но прежде чем приступить к его изготовлению, необходимо составить план (или развертку) материала. В Интернете есть несколько программ для расчета таких узоров. Однако задача настолько проста в решении, что вы можете быстро рассчитать ее с помощью калькулятора (на компьютере), а не искать, скачивать и разбираться с этими программами.

Начнем с простой вариации — разворачивания простого конуса. Проще всего объяснить, как рассчитать деталь, на примере.

Предположим, нам нужно сделать конус диаметром D см и высотой H см. Совершенно ясно, что заготовка будет представлять собой круг с отрезанной одной частью. Известны два параметра — диаметр и высота. Используя теорему Пифагора, рассчитаем диаметр окружности заготовки (не путать с радиусом готового конуса).

円錐）。 Половина диаметра (радиуса) и высота образуют правильный треугольник.したがって：.

Итак, теперь мы знаем радиус детали и можем вырезать круг.

Вычислим угол сектора, который нужно отрезать от круга. Мы рассуждаем следующим образом: Диаметр отрезка равен 2R, поэтому длина окружности равна Pi*2*R — то есть 6,28*R. Обозначим ее через L. Окружность полная, то есть 360 градусов. А длина окружности конечного конуса равна Pi*D. Обозначим его через Lm. Она, конечно, меньше, чем окружность изделия. Нам нужно отрезать отрезок с длиной дуги, равной разнице между этими длинами. Давайте применим правило пропорции. Если 360 градусов дают нам полную окружность детали, то искомый угол должен дать нам длину окружности готового конуса.

Формула соотношения дает величину угла X. А отсекаемый сектор находится путем вычитания 360 — X.

Из круглой детали радиусом R нужно вырезать сектор с углом (360-X). Не забудьте оставить небольшую полоску материала для перекрытия (если вы перекрываете конус). После соединения сторон вырезанного сектора у вас получится конус определенного размера.

Например: Нам нужен конус для вытяжки высотой (H) 100 мм и диаметром (D) 250 мм. Используя формулу Пифагора, получаем радиус фигуры — 160 мм. А длина окружности детали равна 160 x 6,28 = 1005 мм. В то же время длина окружности нужного нам конуса составляет 250 x 3,14 = 785 мм.

Из этого следует, что отношение углов будет: 785 / 1005 x 360 = 281 градус. Сектор 360 — 281 = 79 градусов должен быть отрезан соответствующим образом.

Расчет заготовки выкройки для усеченного конуса.

Эта деталь необходима при изготовлении переходников с одного диаметра на другой или для дефлекторов Вольперта-Григоровича или Ханженкова. Они используются для улучшения тяги в дымоходе или вентиляционной трубе.

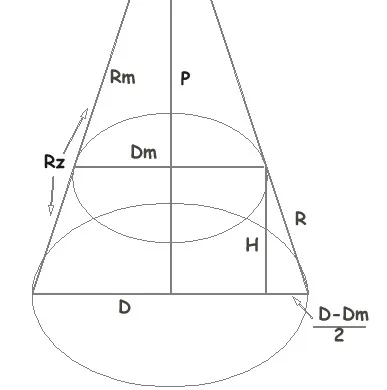
Задача несколько усложняется тем, что мы не знаем высоту всего конуса, а только отсеченной части. В общем случае имеется три исходных элемента: высота конуса H, диаметр нижнего отверстия (основания) D и диаметр верхнего отверстия Dm (в точке полного сечения конуса). Но мы прибегнем к тем же простым математическим построениям, основанным на теореме Пифагора и подобии.

Действительно, очевидно, что величина (D-Dm)/ 2 (половина разности диаметров) связана с высотой конуса пня H, как и радиус основания относительно высоты всего конуса. если не посадить в горшок. Из этого соотношения получается общая высота (P).

От ровного листа до круглой обечайки:

Вальцы с асимметричным расположением роликов (рис. 11) изгибают оболочку почти полностью.

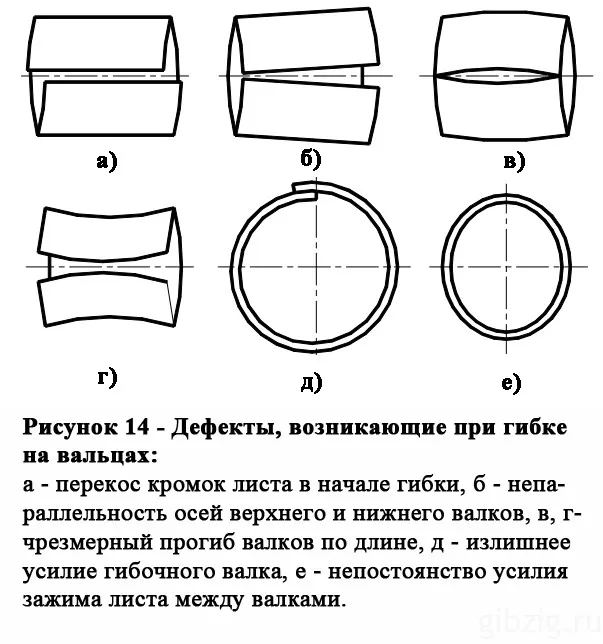
Современные 4-осевые станки (рис. 12) выполняют прокатку и гибку кромок в круговом движении. Радиус изгиба оболочки регулируется стандартом. Дефекты, которые могут возникнуть при прокатке цилиндрических оболочек, показаны на рис. 14.

Конусы и переходные элементы в каждой прочности и качестве материала

Помимо конусов и переходных элементов, производятся все виды оболочек и наполнителей. Там, где это технически возможно, компоненты, которые невозможно транспортировать в целостном виде из-за их размеров, изготавливаются в виде различных частей, которые могут быть собраны на месте для производства конечного продукта.

Высокая точность и надежность в технологии формирования — как раз вовремя

Во время строительства мы уделяем особое внимание превосходному качеству и точности. Существует множество причин, по которым необходимо изготовить конусы из фольги. Металлические конусы используются для закрытия дымоходов, иногда в декоративных целях, даже в случае некоторых видов костров на открытом воздухе или во время барбекю. Не отчаивайтесь, так как складывать металлический лист проще, чем кажется. Входите, конечно, полностью, но осторожно.

Существуют также различные способы получения желаемой формы.

Существует несколько способов сгибания конических оболочек.

1) Установите под углом центральный цилиндр на симметричных трехцилиндровых двигателях и боковые цилиндры на несимметричных трех- и четырехцилиндровых двигателях (рис. 15). 2) Последовательно согните различные части валика (рис. 16) вдоль средней линии. Сначала загибаются края, затем середина детали сгибается в каждой секции путем перестановки. Этот метод приводит к большему износу оборудования.

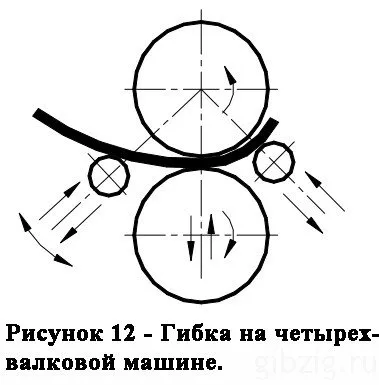
(3) Изгиб оболочек в цилиндрах со сменными коническими цилиндрами. Этот метод оправдан при непрерывном и массовом производстве. (4) Безрулонный метод для листов толщиной до 20 мм. Метод прокатки показан на рис. 17. Края 3 и 4 детали крепятся к опорам 2 и 5 и соединяются вместе, при этом опоры вращаются одновременно в разных направлениях. Затем края конической оболочки свариваются вместе и удаляются машиной. 5) Наиболее производительным методом является изготовление конической оболочки с помощью штампа (рис. 18). Перед сваркой частей оболочки их предварительно фиксируют на месте для предотвращения деформации элементов и обеспечения сварочных расстояний. Края обычно выравниваются с помощью зажимов и монтажных колец для тонких листов (рис. 19). Два зажима располагаются на оболочке с каждого конца.

Цилиндричность оболочки обеспечивается специальным устройством с домкратом, который расправляет деталь. Для сборки негабаритных деталей используются шатуны и клиновые соединения (рис. 20).

Изготовление рабочего конуса на заказ

Карандашом нужно нарисовать круг и отметить небольшую выемку, оставшуюся там, где был установлен компас. 2Вырежьте круг специальными ножницами для металлической фольги. Надевайте перчатки, так как металлические края очень острые. 3Разрежьте круг пополам. Проведите прямую линию с обоих концов, используя опорные точки компаса в качестве опорных и конечных точек. Теперь у вас есть круг из фольги с прорезью, начинающейся с одной стороны и доходящей до центра. Наложите одну сторону четырех прорезей на другую сторону. Начиная с прорези, прижмите куски листа друг к другу. По мере того как вы будете это делать, вы увидите, что круг начинает сжиматься и формировать конус. При необходимости остановитесь. 5 Наклейте ленту на обе стороны накладки. Это предотвращает смещение металла и избавляет вас от неровных краев. Теперь металлический конус лопасти завершен. Всегда надевайте перчатки при работе с металлическими лезвиями, чтобы избежать порезов рук. Ножницы с металлическим лезвием Ножницы с металлическим лезвием Компас Карандаш Рулетка с перчатками. Введение определенных единых правил находит свою справедливую оценку в необходимости обеспечения целей, требуемых аккредитацией профессиональной компетентности в отношении всех профессий, подлежащих аккредитации.

Гибка металла на вальцах

7 декабря 2013 Рубрика: механика|

Недавно я получил несколько запросов от читателей этого блога с просьбой помочь решить одну и ту же проблему: как определить конечное положение среднего ролика (валка) при работе с прессованными трехцилиндровыми вальцами и профилегибами …

… По отношению к положению концевого ролика, который изгибает (прокатывает) деталь до заданного требуемого радиуса? Ответ на этот вопрос заключается в повышении производительности при гибке металла и уменьшении количества проходов детали до получения хорошей детали.

В этой статье вы найдете теорию

решение этой проблемы. Должен признаться, что я не применял этот расчет на практике и, соответственно, не проверял эффективность предложенного метода. Однако этот метод может быть использован для сгибания металла гораздо быстрее, чем обычно.

В большинстве случаев окончательное положение подвижного центрального вала (валика) и количество проходов для получения хорошего изделия определяются «методом метра», как это обычно и бывает. После длительной (или не очень длительной) обработки тестового образца определяется положение центрального ролика (валика). Это используется для дальнейшей регулировки валков и производства партий этих изделий.

Этот метод удобен, прост и подходит для многих одинаковых компонентов, т.е. для непрерывного производства. При производстве единичных или «очень малых партий», когда листы разного профиля или разной толщины необходимо согнуть под разным радиусом, время, необходимое для настройки кассы, может оказаться катастрофическим. В частности, эти потери могут происходить при изгибе длинных (8 … 11 м) куски во время сгибания! Во время создания путей … во время проведения измерений … … при восстановлении положения цилиндра (цилиндра) … И снова! Десятки раз.

Расчет в Excel местоположения подвижного среднего ролика

Запустите MSExcel или OOoCalc и начните работу.

Общие правила форматирования электронных таблиц, применимые к записям в блоге, можно найти здесь.

Во-первых, различные модели листогибочных и профилегибочных вальцов и профилегибочных станков имеют подвижный концевой ролик (валик) и подвижный средний ролик (валик). Однако в нашем случае это не имеет принципиального значения.

Следующая диаграмма иллюстрирует рассматриваемую схему расчета.

Прокатная полоса в начале процесса находится на двух внешних роликах (вальцах) диаметром D.

. Средний цилиндр (цилиндр) диаметром d переносится в верхнюю часть детали.

Затем средний ролик (цилиндр) опускается на расстояние, равное расчетному размеру H

Активируется вращение ролика, прокатная деталь, металл сгибается и на выходной части рассчитывается требуемый радиус изгиба R! Мы делаем это следующим образом.

Исходные данные:

1. диаметр/ссылка/d верхнего цилиндра, который необходимо переместить

Клетчатка D3: 120

2. диаметр приводного наружного ролика (валика) d

D4 на клетку: 150

Учрежден сертификат профессиональной компетентности, соответствующий профессии промышленного горельщика, тяжелой промышленности и металлоконструкций, который является официальным и действительным на всей территории страны.

Боковой профиль линейного конуса представляет собой форму веера, радиус которого равен длине конической поверхности l. Центральный угол φ определяется по формуле φ = 360 * R / l где R — радиус основания окружности конуса.

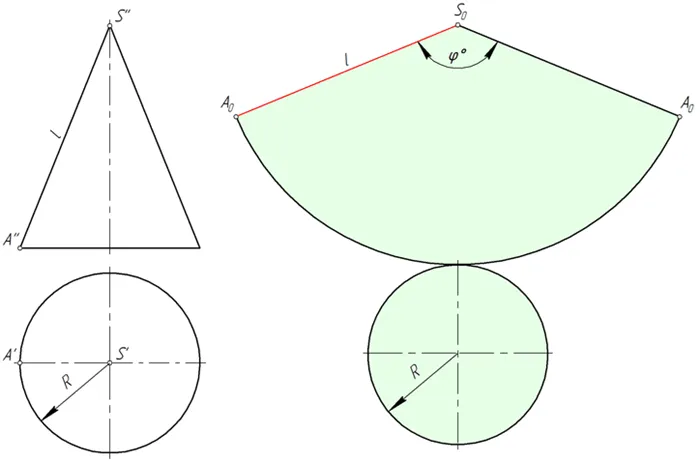
В некоторых задачах начертательной геометрии предпочтительным решением является приближение (замена) пирамиды гравированным конусом и построение приближенной развертки, удобной для рисования линий на поверхности конуса.

1. На конической поверхности написана многоугольная пирамида. Чем больше граней пирамиды вписано, тем точнее соответствие между реальным и приблизительным сканированием.
2. Нарисуйте развертку сторон пирамиды, используя метод треугольника. Соедините точки, принадлежащие основанию конуса, плавной кривой.

На рисунке ниже правильная многоугольная пирамида SABCDEF вписана в прямой конус, а примерное развитие ее граней состоит из шести равнобедренных треугольников, которые являются гранями пирамиды.

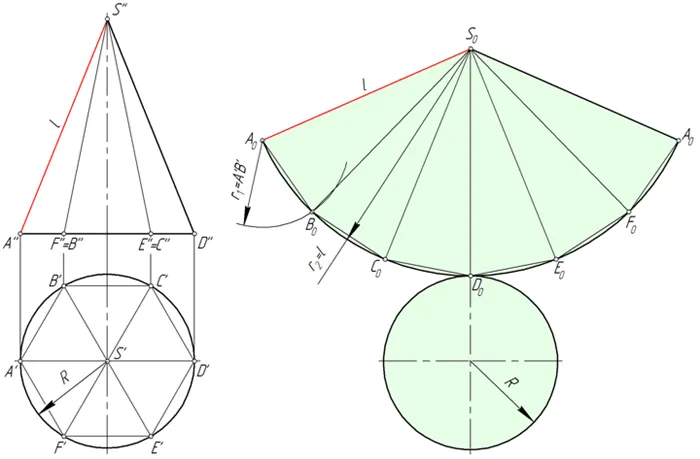
Рассмотрим треугольник S₀A₀B₀. Длина сторон S₀A₀ и С₀B₀ равна модулю упругости l конической поверхности. Значение A₀B₀ соответствует длине A’B’. Для построения треугольника S₀A₀B₀ Предельное сечение S в любой точке чертежа₀A₀= l, тогда из S₀ и А₀ определяют окружность радиуса S₀B₀= l и A₀B₀= A’B’ соответственно. Соедините точки пересечения окружностей B₀ вместе с₀ и С₀Точки A, B, C, D, E и F в основании конуса соединены плавной кривой, которая является дугой окружности с радиусом, равным l.

Путем приближения исследуется порядок построения сторон наклонного конуса.

Развертка наклонного конуса

Напишите шестиугольник 123456 на основной окружности конуса. Соедините точки 1, 2, 3, 4, 5 и 6 с верхней S. Построенная таким образом пирамида S123456 в какой-то степени заменяет коническую поверхность и будет использоваться в этом качестве в будущих постройках.

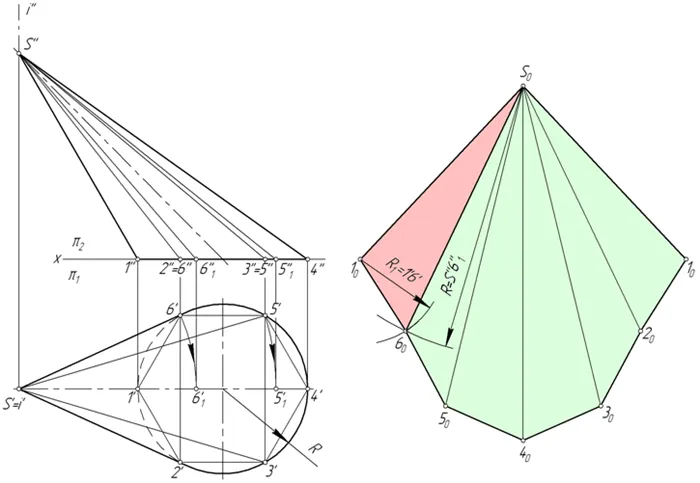
1. Используя метод вращения вокруг проецируемой прямой, определяются натуральные значения граней пирамиды: в данном примере ось i перпендикулярна горизонтальной плоскости проекции и проходит через вершину S. Новый горизонтальный вид вращения S’5′ ребра S5
2. Занимает положение, параллельное фронтальной плоскости π₁S»’ 5». Следовательно, S» 5»₂ -это физическая величина S5.₁Создайте скан боковых граней пирамиды S123456, состоящей из шести треугольников; S
3. , S₀1₀6₀, S₀6₀5₀, S₀5₀4₀, S₀4₀3₀, S₀3₀2₀, S₀2₀1₀ Длина S₀1₀6₀= S» 1»₀1₀, S₀, S₀6₀, 1₁= 1’6».₀6₀Степень соответствия подхода реальному зависит от количества вырезанных поверхностей пирамиды. Количество поверхностей выбирается исходя из разборчивости рисунка, требований к точности и наличия характерных точек и линий, которые необходимо перенести на колесо.

Линия n на поверхности конуса образуется в результате его пересечения с плоскостью (см. ниже). Рассмотрим алгоритм создания линии n на колесе.

Перенос линии с поверхности конуса на развертку

Найдите проекции точек A, B и C, в которых прямая n пересекает ребро конуса пирамиды S123456.

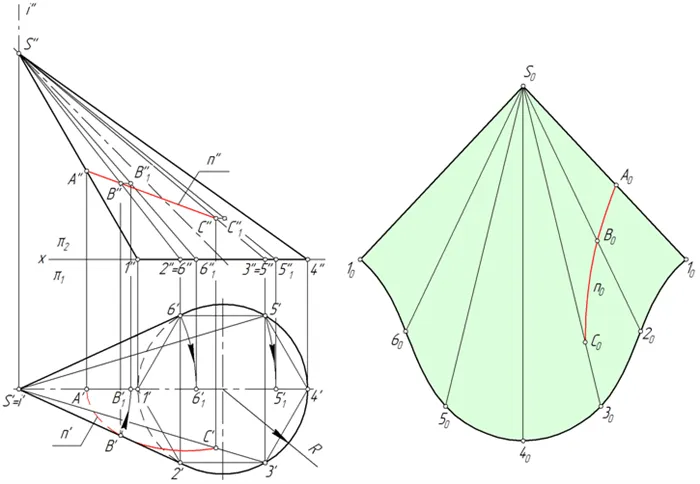
1. Поверните проекционную линию вокруг центра и определите физические размеры отрезков SA, SB и SC. В данном примере SA = S»A», SB = S»B».
2. , SC = S»’C»’₁.₁Точки A, B, C, D, E и F в основании конуса соединены плавной кривой, которая является дугой окружности с радиусом, равным l.
3. , B₀, C₀ Соответствующие ребра пирамиды, используя диаграмму в разделе S₀A₀A₀B₀B₀, S₁, S₀= S» C»₀.₁Точки A, B, C, D, E и F в основании конуса соединены плавной кривой, которая является дугой окружности с радиусом, равным l.
4. , B₀, C₀ Соответствующие ребра пирамиды, используя диаграмму в разделе S₀Чтобы определить степень конуса, введите значения максимального диаметра конуса, минимального диаметра конуса и длины конуса и нажмите кнопку Calculate.

Как вы можете себе представить, конус образован двумя различными поверхностями. Один — плоский круг у основания. Предположим, что она имеет радиус r. Вторая поверхность является боковой и называется конусом. Предположим, что его форманта равна g.

Вид развертки конуса

Если у вас есть бумажный конус, вы можете вырезать основание ножницами. Затем коническую поверхность необходимо разрезать по форманте и разровнять. Таким образом, на боковых сторонах конуса можно сделать скользящие поверхности. На следующем рисунке показаны две поверхности вместе с исходным конусом.

Основной круг показан в правом нижнем углу. Расширенная коническая поверхность нарисована посередине. Видно, что он соответствует определенному круговому сегменту окружности, радиус которого равен длине g гениталий.

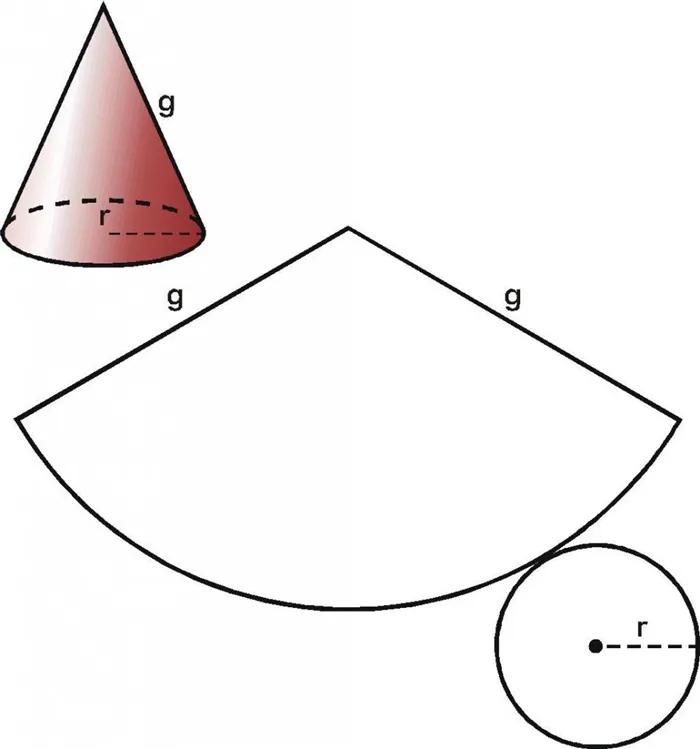
Теперь, учитывая известные параметры g и r, у нас есть уравнение, позволяющее вычислить площадь и угол расширенного конуса.

Угол и площадь развертки

Очевидно, что длина веерообразной дуги, показанной на диаграмме выше, равна длине основной окружности. Это означает, что

Если создать целую окружность радиуса g, то ее длина составит

Если длина L соответствует радиусу 2*pi, то угол, на который опирается дуга l, можно определить из соответствующего соотношения.

В этом случае неизвестный угол φ становится равным

Подставив уравнения для длин l и L, получим выражение для угла, образованного сторонами конуса.

Угол φ выражается здесь в терминах радиуса.

Значение φ используется для определения площади Sb веерной формы. Только для области создается другое соотношение. У нас есть:.

Отсюда выражаем Sb и заменяем значение угла φ. У нас есть.

Sb = φ*g2* pi / (2 * pi) = 2 * pi * r / g * g2 / 2 = pi * r*g.

Для площади поверхности конуса мы получили достаточно надежное выражение. Значение Sb равно произведению трех факторов: окружности, радиуса фигуры и ее форманты.

Тогда площадь всей поверхности равна сумме Sb и So (площадь основания круга). Получаем следующее уравнение

Для решения этой задачи вам понадобится лист бумаги, карандаш, углошлифовальная машина, линейка и компас.

Построение развертки конуса на бумаге

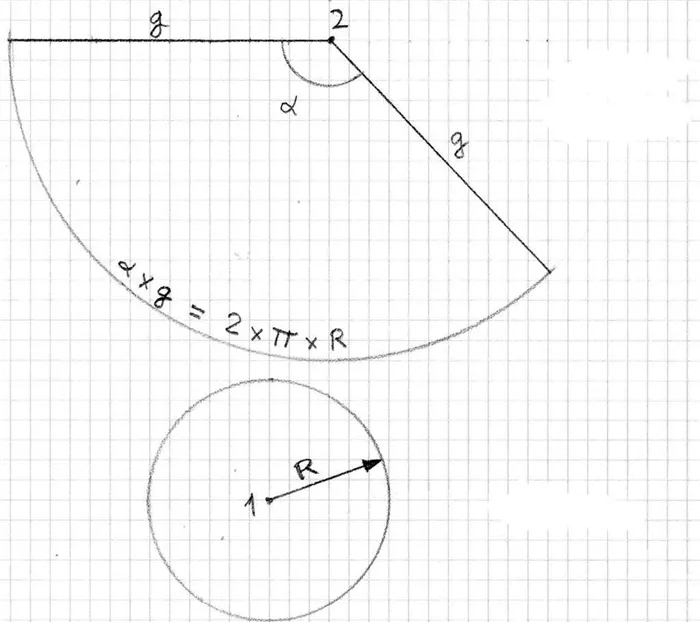
Сначала начертите прямоугольный треугольник со сторонами 3 см, 4 см и 5 см. Вращение вокруг катетера на 3 см дает искомый конус. На диаграмме показаны r = 3 см, h = 4 см и g = 5 см.

Мы начинаем проектировать рейлинги с помощью компаса. Его длина будет равна 6*pi см. Теперь мы проектируем еще один круг, но уже с g. Его длина будет равна 10*pi см. Теперь нужно вырезать круглый сектор из большего круга. Угол ϕ равен: ϕ = 1,5*pi см.

Затем обозначим этот угол с помощью циркуля G — радиуса с помощью транспортира и проведем два луча, ограничивающих круговой сектор.

Теперь вы создали профиль конуса с необходимыми параметрами радиуса, высоты и конфигурации.

Разработка конуса