Нахождение значений синуса, косинуса, тангенса и котангенса. Как рассчитать градус угла

В некоторых случаях для нахождения sin или cos угла можно использовать соответствующее уравнение триангуляции. Например, если вам известно значение синуса 45°, вы можете использовать формулу триангуляции для определения значения синуса 30°.

Таблица градусов и углов, с примерами решений

В этой статье мы рассмотрим таблицы полутонов, косинусов, тангенсов и триангуляции четырехугольников. 0.30, 45, 60, 90, … и 360-градусных углов для изучения основных понятий тригонометрических функций.

Затем посмотрите, как эти таблицы можно использовать для вычисления тригонометрических величин. Сначала рассмотрите таблицы косинуса, синуса, тангенса и четырехугольника от углов 0, 30, 45, 60 и 90 градусов.

Определение этих величин дает нам функции угла при 0 и 90 градусах.

• sin 00 = 0, cos 00 = 1. tg 00 = 0, касательная из 00 становится неопределенной sin 900 = 1, cos 900 = 0, ctg900 = 0, касательная из 900 становится неопределенной.
• Если взять правильный треугольник с углами от 30 до 90 градусов. Мы получаем:.
• sin 300 = 1/2, cos 300 = √3/2, tg 300 = √3/3, ctg 300 = √3sin 450 = √2/2, cos 450 = √2/2, tg 450 = 1, ctg 450 = 1 sin 600 = √3/2, cos 600 = 1/2, tg 600 = √3, ctg 600 = √3/3
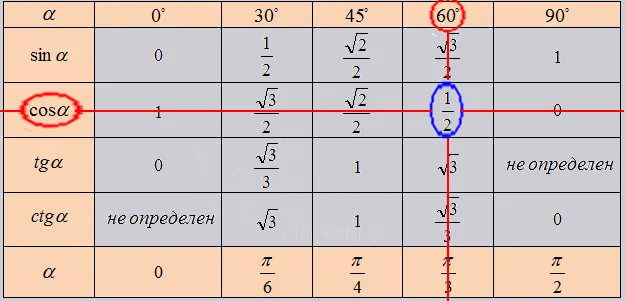
• Выразите все полученные значения в виде таблицы тригонометрии: см. таблицу ниже.

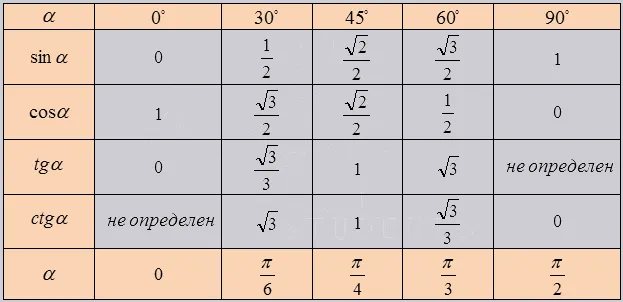
1. Использование формулы уменьшения увеличит размер массива и добавит значения для углов до 360 градусов. Хорошим примером этого является следующее.

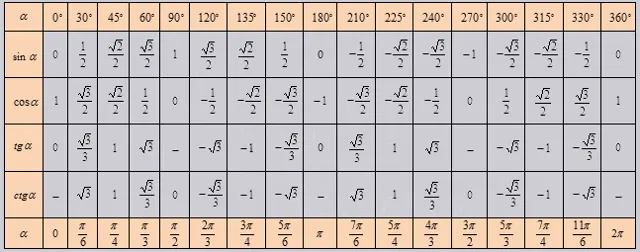
Также, исходя из свойства цикличности, углы равны 00 + 3600 * z ….. Массив можно увеличить, заменив 3300 + 3600 * z где z — целое число. Используя эту таблицу, вы можете вычислить все значения углов от соответствующих точек в пределах одной окружности.

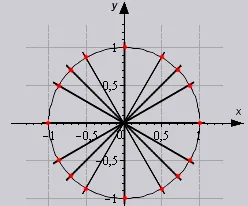
Давайте посмотрим, как использовать таблицу в решении. Все очень просто. Это происходит потому, что нужные вам значения находятся на пересечениях вычисляемых ячеек. Например, если взять угол cos равный 60 градусам, то таблица будет иметь следующий вид

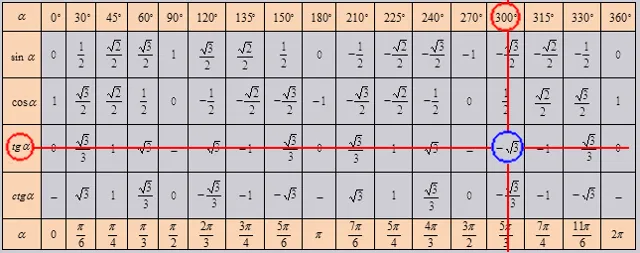
В сводной таблице основных значений для тригонометрических функций можно действовать аналогичным образом. Однако в этой таблице мы можем найти значение тангенса от угла в 1020 градусов. Это = -√3 контроль 10200 = 3000 + 3600*2. Поиск по таблице.

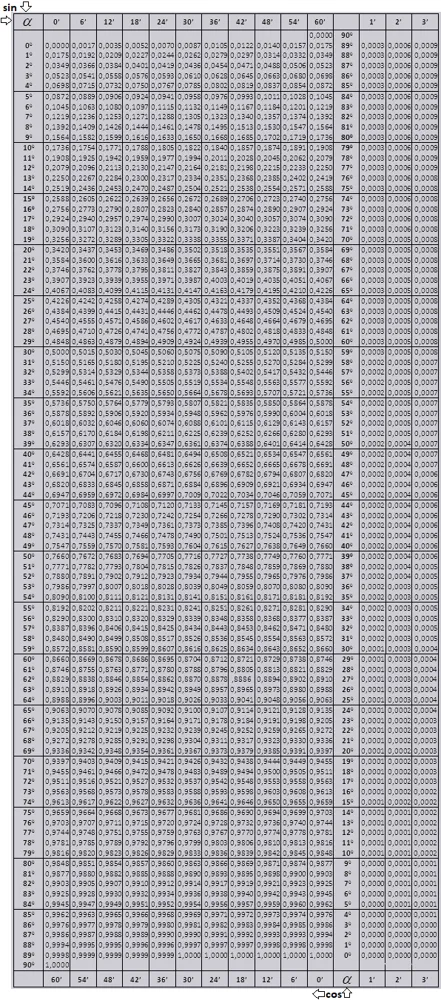
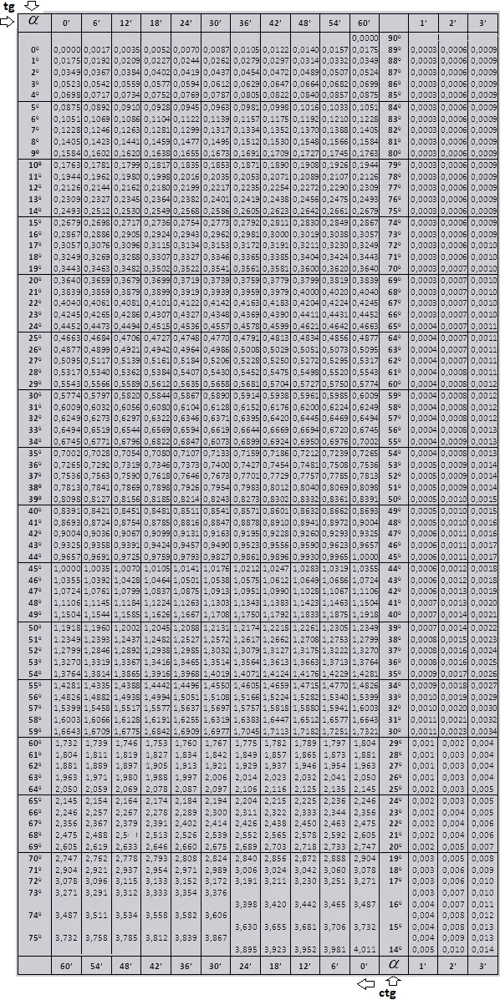
Чтобы найти значение триангуляции для ближайшего минутного угла, используйте таблицы Брадиса. Подробные инструкции по их использованию можно найти по ссылке.

Стол Брадиса. Косинус, тангенс и четырехугольник для полутонов.

• Доска Брадиса разделена на несколько частей, состоящих из панели косинусов, панели синусов, панели тангенсов и панели пятиугольников. Они делятся на две части (максимальный угол tg 90° и малый угол ctg).
• Полутона и косинусы.

Измерение углов

Когда линии пересекаются, существуют четыре различные области относительно точки пересечения. Эти новые области называются углами.

Углы больше 360 градусов

Когда объект рисует полный круг вокруг точки, он образует 360°, но когда объект делает несколько кругов, он образует угол больше 360°, сказал. Это обычное явление в повседневной жизни. При движении автомобиля, т.е. колеса, оно образует угол больше 360°.

Чтобы найти количество окружностей (проходящих кругов) при вращении объекта, подсчитайте, сколько раз ему нужно прибавить к себе 360, чтобы получить число, меньшее заданного угла. Аналогично, умножьте число на 360, чтобы получить число, которое мало, но близко к определенному углу.

• Пример 21.Найдите число циклов, описываемых объектом, образующим угол a) 380° b) 770° c) 1000°
• Решение.

(a) 380 = (1×360) + 20 объект описывает цикл, а 20° = 20^ = frac = frac $ $ frac $ объект описывает 400 frac $ цикла. (b) 2×360 = 720 770 = (2×360) + 50 объект описывает два цикла и 50° $ 50^ = frac = frac $ окружности. = 720 1000 = (2×360) + 280 $ 280^ = frac = frac $ предложение

Положительные и отрицательные углы

При вращении объекта по часовой стрелке образуется отрицательный угол поворота, а при вращении против часовой стрелки — положительный. До сих пор рассматривались только положительные углы.

Это означает, что если существует отрицательный угол, то он может иметь соответствующий положительный угол. Например, нижняя часть вертикальной линии равна 270°. Измеряя в отрицательном направлении, мы имеем -90°. Просто удалите 270 из 360. Если угол отрицательный, прибавьте 360, чтобы получить соответствующий положительный угол.

1. Если угол равен -360°, это означает, что объект совершил несколько кругов по часовой стрелке.
2. Пример 3 1. Найдите соответствующий положительный угол a) -35°b) -60°c) -180°.
3. (d) -670°.

2. найдите соответствующие отрицательные углы 80°, 167°, 330° и 1300°. Решение 1. Прибавьте 360 к цене угла, чтобы найти соответствующий положительный угол. (A) -35° = 360 + (-35) = 360 -35 = 325°B) -60° = 360 + (-60) = 360 -60 = 300°) -180° = 360 + (-180) = 360 -180 = 180°D) -670° = 360 + (-670) = -310 Это означает, что по часовой стрелке (360) 360 + (-310) = 50°.

2. чтобы получить соответствующий отрицательный угол, отнимите 360 от угла наклона. 80° = 80-360 = -280°167° = 167-360 = -193°330° = 330-360) 580-360 = 220 (третий круг завершен) 220-360 = -140° угол есть угол -360-360-360-140 = -1220°

Радианная и градусная мера угла

Здесь мы видим описание проблемы PROC32 -PROC33 из задач Аврамиана: возможность преобразования угла из градуса в радиус.

Так что же такое радиальная мера угла? Рассмотрим окружность радиуса r с центром O. Цикл делится на 360 градусов и имеет длину 2PR, поэтому длина лука составляет 2PR/360 = PR/180 на градус. Тогда угол a градусов соответствует длине дуги l = pra/180.

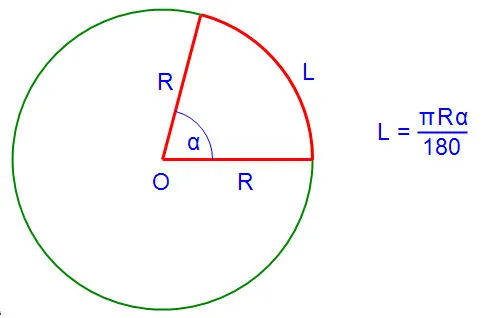
В этом смысле очень интересно, если длина дуги l равна радиусу r. Каков угол наклона носовой части в этом случае? Вспоминая предыдущий тип расчета длины лука, имеем pra/180 = r, pa/180 = 1 и, следовательно, α = 180/p.

• Таким образом, если длина лука равна радиусу окружности, то соответствующий угол равен 180/p. Этот угол называется радиусом (rad).
• 1 рад = 180/п.
• Итак.
• Rynia = 180° и 1° = pi/180 лучей.
• Радиальная мера угла — это мера угла, где 1 рад — угол дуги, равный радиусу этой дуги. Поскольку 1 радиус соответствует длине дуги, равной радиусу, возникают следующие выводы.
• Величина радиусомера угла равна отношению длины окружности к радиусу этого цикла.

Например, если длина ARC составляет 1,5R, радиальный диаметр угла этого лука составляет 1,5-0,25R, то радиальное измерение лука длиной 2PR составляет 0,25-. (полный цикл) Радиальное значение измерения составляет 2p и т.д. В общем случае, для длины отрезка угол l/r равен l/r, где r — радиус.

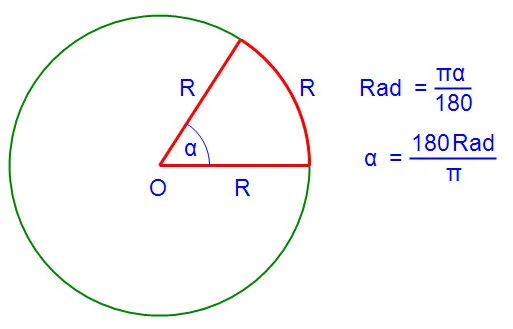
Радиус — очень удобный способ измерения углов, так как вместо самого угла можно использовать отношение длины дуги к ее радиусу. В высшей математике все тригонометрические функции используют только радиальные меры.

Proc32: Если значение D задано в градусах (D — вещественное число, 0≤Dhttps://progmatem.ru/proc/), напишите функцию DegToRad (D) вещественного типа, которая находит значение угла в радиусе. proc-32-33.html.

Затем снова посчитайте, посчитайте, а затем, например, прибавьте 85 к сохраненным 145 и нажмите M+ или M-, чтобы вычесть 85 из сохраненных 145. В первом случае нажмите MR для возврата. Общее число из памяти — 230; во втором случае нажатие M- и MR возвращает 60.

Линии тригонометрических функций

Тригонометрические линии — это линии, которые отображаются с помощью единичной окружности. Они имеют опорную точку и единичный отрезок, равный 1 в системе координат. Они используются для визуального представления значений.

Изучите их подробно

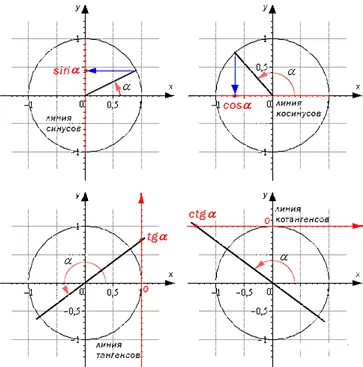
Как найти sinα, cosα, tgα и ctgα

Существуют конкретные значения для углов 30, 40 и 60 градусов. Чтобы найти их, можно воспользоваться правилом правильного треугольника с острыми углами. Для этого используется теорема Пифагора.

Чтобы найти значения углов 30° и 60°, начертите прямоугольный треугольник с углами определенной величины. Длина гипотенузы должна быть равна 1. Согласно теореме Пифагора, катет на противоположной стороне 30-градусного угла равен половине косой стороны. Воспользуемся теоремой: 1 2- 1 2 2 =32. Поскольку синус угла — это деление перпендикуляра с наклонной стороной, вычисляем sin30° = 1 2 1 =12 и sin60° = 32 1 =32.

Косинус можно найти по формуле, предполагающей, что соседние категории делятся по диагонали. Вычислите cos30°=32 1 =32 и cos60°=12 1 =12.

Касательные можно найти в уравнениях, которые предполагают деление противоположных перпендикулярных линий на соседние перпендикулярные линии. Котенер находится по той же формуле. Разделите соседние на противоположное уравнение.

Вычислите tg30° = 12 3 2 = 1 3 =33 и tg60° = 32 1 2 =3. Найдите косинусы по аналогичной схеме: tg30°=32 1 2=3 и tg60°=12 3 2 = 1 3 =33. Затем перейдите к вычислению значений основных тригонометрических функций для угла 45°. Используйте равнобедренный треугольник с углом 45° и косой стороной 1. Используйте теорему Пифагора. Согласно формуле, длина катетера равна 22. Т

Теперь мы можем найти значение основной тригонометрической функции. Используйте формулу, предполагая, что длины соответствующих сторон этого треугольника кратны.

Получается следующее уравнение: c tg45°=22 2 2 2=1.

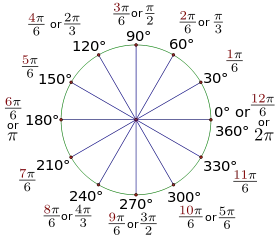
Значения, полученные для углов 30, 45 и 60 градусов, могут быть использованы для решения различных задач. Запишите их — вы будете использовать их часто. Для удобства можно использовать таблицу значений.

Используйте окружности и линии, чтобы показать значения углов 30, 45 и 60 градусов.

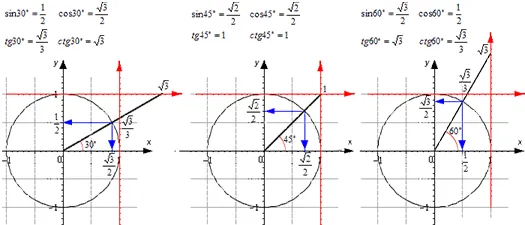
Значения основных функций тригонометрии

Основные тождества из геометрии относятся к sinα, cosα, tgα и ctgα определенного угла. Используя одну функцию, легко найти остальные.

Чтобы найти синус при известном синусе, sin2α+cos2α=1.

Угол с известным синусом tg2α+1=1cos2α.

Квадратичный от известного полутона или наоборот 1 + ctg2α=1sin2α.

Тангенс через катенар или наоборот можно найти благодаря удобной формуле: t g a — c t g a = 1 .

Чтобы закрепить полученные знания, давайте рассмотрим подробный пример

Найдите значение синуса угла π 8 , если t g π 8 = 2 — 1 .

Сначала найдите котангенс угла: c t g π 8 = 1 t g π 8 = 1 2 — 1 = 2 + 1 ( 2 — 1 ) — ( 2 + 1 ) = 2 + 1 ( 2 ) 2 — 1 2 = 2 + 1 По формуле 1 + c t g 2 α = 1 sin 2 α. С его помощью мы вычислим значение синуса. Имеем sin 2 π 8 = 1 1 + c t g 2 π 8 = 1 1 + ( 2 + 1 ) 2 = 1 4 + 2 2 = 1 2 — ( 2 + 2 ) = 2 — 2 — 2 — ( 2 + 2 ) — ( 2 — 2 ) = = = 2 — 2 2 2 — ( 2 — ( 2 — ( 2 ) 2 ) = 2 — 2 4

Для завершения необходимо определить значение синуса. Угол π 8 — это угол первой четверти, тогда синус положителен. Чтобы определить точный знак, можно воспользоваться таблицей, определяющей знаки по квадрантам координатной плоскости. Поэтому sin π 8 = sin 2 π 8 = 2 — 2 4 = 2 — 2 2. sin π 8 = 2 — 2 2 2 2 .

Сведение к углу

Удобнее находить значения для угла от 0 до 90°. Уменьшите угол от 0 до 90°. Если угол не соответствует заданному интервалу, мы можем использовать законы и тождества, которые мы изучали на уроках геометрии. Тогда мы сможем найти значение, равное углу в заданных пределах.

Задача состоит в том, чтобы найти синус 210°. Представим 210 в виде разности или суммы, разбив число на различные части. Используйте соответствующую формулу для уменьшения. Используем формулу для нахождения значения синуса 30° : sin 210° = sin ( 180° + 30° ) = — sin 30° = — 1 2 , или косинус 60° sin 210° = sin ( 270° — 60° ) = — cos 60° = — 1 2 .

Чтобы облегчить решение задач, при нахождении значений переходите к углам от 0° до 90°, используя формулы приведения, если угол не находится в этих пределах.

Например, если длина ARC составляет 1,5R, радиальный диаметр угла этого лука составляет 1,5-0,25R, то радиальное измерение лука длиной 2PR составляет 0,25-. (полный цикл) Радиальное значение измерения составляет 2p и т.д. В общем случае, для длины отрезка угол l/r равен l/r, где r — радиус.

Углы в 30 и 45 градусов

Выбрав один из способов вычисления 90-градусного угла с помощью рулетки, нетрудно образовать три варианта острых углов. 45 градусов получается, если это равнобедренный треугольник. Для 30 градусов нужно продлить гипотенузу, которая будет равна двум коротким перпендикулярам. Здесь угол между ними остается равным 60 градусам.

В этом видеоролике учитель делится своим опытом выведения прямых углов с помощью теоремы Пифагора и египетского треугольника:

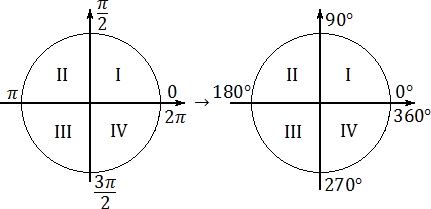
Коротко главном

В интерьерах часто возникает необходимость провести прямые углы под мебелью или сантехническими приборами.

Существует три способа проверки угла 90 градусов с помощью рулетки: Стороны составляют 3/4/5 частей, если соединительная линия между метровыми стенами равна 141,4 см, применяя теорему Пифагора.

Рулетки также достаточно для формирования трех углов в 30, 45 и 60 градусов.

Кроме того, вам может понадобиться только калькулятор и карандаш для выставления оценок.

Помните: в 8-9 классах мы работали только с несколькими стандартными углами. В частности: 30°, 45° и 60°. В особо продвинутых случаях учителя также говорили об углах 90° и 0°. Любые другие значения назывались «сложными», и появление таких углов, скорее всего, указывало на ошибку в решении.

Как пользоваться инженерным калькулятором – на примерах

Как возвести в степень

Чтобы задать, например, 12^3, введите следующую последовательность:

12 x y 3 =

12, ключ «x в степени igric» xy, 3, символ равенства =

Как найти корень кубический

Предположим, мы извлекаем кубический корень из 729, нажимая в таком порядке:

729, 3 √x «кубический корень из x», равен =

Как найти корень на калькуляторе

Проблема: Найдите квадратный корень из 36.

Решение: все просто, нажмите вот так:

36 y √ x 2 =

36, y √x «квадратный корень из x, в степени igric», нужная нам степень равна 2, равна = = =

Вы можете использовать эту функцию для нахождения корня из любой силы, а не только квадратного корня.

Как возвести в квадрат

Программа онлайн-калькулятора содержит две функции для возведения в квадрат:

x y «x в степени igric», x 2 «x в квадрате».

Последовательность ввода такая же, как и раньше — сначала вводится начальное значение, затем «x^2» и символ равенства, или, если это не квадрат, а произвольное число, нужно нажать «x^y», затем указать нужную мощность и точно так же нажать символ равенства.

Например: 45 x y 6 =

Ответ: сорок пять в шестой степени равно 8303765625

Тригонометрический калькулятор онлайн — примеры

Как произвести онлайн расчет синусов и косинусов, тангенсов

Обратите внимание, что kalkpro.ru умеет работать как в градусах, так и в радианах и градусах.

1 рад = 57,3°, 360° = 2п радиан, 1 градус = 0,9 градуса или 1 градус = 0,015708 радиан.

Нажмите соответствующую кнопку для переключения между двумя режимами измерения:

Где Deg — градусы, Rad — измерение в радианах, Grad — измерение в градусах. По умолчанию установлено значение градусов.

В качестве простейшего примера, давайте найдем синус 90 градусов.タイプ：：：：.

Вычисляются и другие тригонометрические функции, например, вычислим косинус 60°:

Обратные тригонометрические функции вычисляются аналогичным образом онлайн в CALCPRO — arcsinus , arccosine, arctangens, и гиперболические функции sinh, cosh, tanh.

Для их импорта необходимо изменить интерфейс, нажав Inv, появятся новые кнопки — asin, acos, atan. Порядок ввода такой же, как и раньше: сначала значение, затем символ нужной функции, либо acrssinus, либо arcsinus.

Преобразование с кнопкой Dms и Deg на калькуляторе

Deg преобразует угол из градусов, минут и секунд в десятичные градусы для вычислений. Dms выполняет обратный перевод — в виде «градусы, минуты, секунды».

Например, угол 35 o 14 минут 04 секунды преобразуем в 53 десятые доли секунды:

35,140453 градуса = 35,234591666666666666666666666666

Перевести в старый формат: 35,234591666666666666666666666666666666 Dms = 35,140453

Десятичный логарифм онлайн

Десятичный логарифм в калькуляторе вычисляется следующим образом, например, ищите единицы логарифма в основании 10, log10(1) или lg1:

Оказалось, что это 0. Чтобы рассчитать lg100, нажмите кнопку :

Решение. Как вы проверяете себя? Что такое десятичный логарифм в общем случае — log по основанию 10. В нашем примере 2 — это степень, в которую нужно ввести основание логарифма, то есть 10, чтобы получить 100.

Натуральный логарифм вычисляется таким же образом, но с помощью кнопки ln.

Как пользоваться памятью на калькуляторе

Существующие кнопки памяти: M+, M-, MR, MS, MC.

MS используется для добавления данных в память программы для дальнейших вычислений.

MR отобразит информацию, сохраненную в памяти. MC удалит все данные из памяти. M- вычтет число на онлайн-дисплее из числа, сохраненного в памяти.

例 。 Введите в память программы сто сорок пять:

После выполнения других вычислений нам вдруг понадобится вернуть запомненное число на экран онлайн-калькулятора, просто нажмите кнопку :

На дисплее снова отобразится 145.

Затем снова посчитайте, посчитайте, а затем, например, прибавьте 85 к сохраненным 145 и нажмите M+ или M-, чтобы вычесть 85 из сохраненных 145. В первом случае нажмите MR для возврата. Общее число из памяти — 230; во втором случае нажатие M- и MR возвращает 60.

Инженерный калькулятор kalkpro.ru выполняет сложные расчеты быстро и точно, значительно упрощая ваши обязанности.