Как находить внешний угол. Как находить внешний угол

Основное свойство: внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Это свойство доказывается довольно просто. Сумма смежных углов равна 180. Сумма углов треугольника равна все тем же 180. Тогда, если внутренние углы равны a, b, c, а внешние — d, то

Как найти внешний угол многоугольника

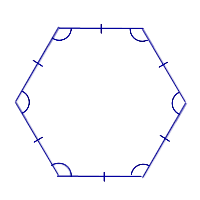
Внутренний угол многоугольника — это угол, образованный двумя соседними сторонами многоугольника. Например, ∠ABC — это внутренний угол.

Внешний угол многоугольника — это угол, образованный продолжением одной стороны многоугольника другой стороной. Например, ∠LBC является внешним углом.

Количество углов в многоугольнике всегда равно количеству сторон. Это относится как к внутренним, так и к внешним углам. Можно построить два равных внешних угла для каждой вершины многоугольника, но всегда рассматривается только один из них. Поэтому, чтобы найти количество углов многоугольника, необходимо подсчитать количество его сторон.

Сумма внутренних углов

Сумма внутренних углов выпуклого многоугольника равна произведению 180° и числа сторон, исключая 2.

Здесь s — сумма углов, 2d — два прямых угла (т.е. 2-90 = 180°) и n — количество сторон.

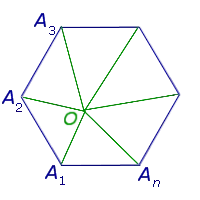
Если из вершины A многоугольника ABCDEF проведены все возможные диагонали, то многоугольник делится на два треугольника меньше, чем число сторон многоугольника.

Поэтому сумма углов многоугольника равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна 180° (2 d), то сумма углов всех треугольников равна произведению 2 d и их количества.

Из этого уравнения видно, что сумма внутренних углов постоянна и зависит от количества сторон многоугольника.

Угол λ является смежным с внешними углами и вычисляется по следующей формуле (в соответствии со свойствами внешних углов): λ = 180° — γ = 180° — 115° = 65° ……..

Определение 5. Два угла называются смежными, если они имеют общее ребро и их сумма равна 180° (рис. 1).

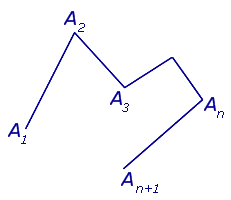
Определение 6. Внешний угол многоугольника — это угол, прилежащий к внутреннему углу многоугольника (рис. 2).

Свойства углов треугольника

Сумма углов треугольника равна 180°.

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним

Углы треугольника.

Сумма углов треугольника равна 180°.

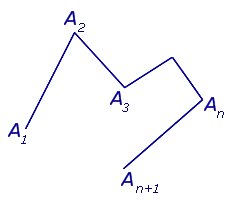
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним

Давайте введем еще одно понятие — прямоугольные треугольники. Поскольку мы говорим о типах треугольников и углах, нам необходимо поговорить о правильных треугольниках.

Свойства внешнего угла

Это не означает, что существует множество свойств внешних углов. В основном, когда речь идет о внешних углах, для решения или доказательства задачи достаточно теоремы о внешних углах треугольника. Ну, а также смежность внутренних и внешних углов.

Другими словами, основное определение.

Однако, когда задействованы биссектрисы, свойства внешних углов открываются в дополнение к «классическим» свойствам. Рассмотрим один из самых полезных.

Свойства биссектрис внешнего и внутреннего углов треугольника. Биссектрисы внутреннего и внешнего углов перпендикулярны друг другу.

Доказательство.

В треугольнике $bigtriangleup$ проведите биссектрисы внешнего $угольника$ и внутреннего $угольника$. Для удобства обозначьте все углы, полученные следующим образом: $x$ и $y$ — внутренние углы при вершинах $A$ и $C$ соответственно, $z$ — половина внутреннего угла$ и $f$ — половина внешнего угла$.

Необходимо установить, чему эквивалентны $Z+F$. Если сумма равна $90^circ$, то свойство доказано. Воспользуемся теоремой о внешних углах и теоремой о сумме углов треугольника.

Нам нужно найти только сумму $z+f$, поэтому дополним вышеприведенное уравнение.

Находим, что 3500(f+z)=180^Circ$ после уменьшения.

Поэтому сумма $f$ и $z$ равна $90^

Задача для самостоятельного решения

Свойством внешних углов треугольника является. Теорема о внешних углах треугольника однозначна — да. Решите эту задачу, не используя свойство смежности внешних и внутренних углов.

Состояние В треугольнике $bigtriangleup$ размеры внешних углов $angle$ и $angle$ равны $97^circ$ и $125^circ$ соответственно. Найдите, чему соответствует внутренний угол $$.

Таким образом, если многоугольник имеет n сторон (и n вершин), то сумма внешнего и внутреннего углов при всех n вершинах равна 2 dn. Чтобы из этой суммы 2 dn получить только сумму внешних углов, вычтите сумму внутренних углов, то есть 2d(n — 2).

Формулировка теоремы

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

Из этой теоремы следует, что внешний угол треугольника больше его внутреннего угла, не являющегося смежным.

Примеры задач

Задача 1 Известно, что треугольник имеет два угла, 45° и 58°. Найдите внешний угол, прилежащий к неизвестному углу треугольника.

Решение Используя формулу теоремы, имеем: 45° + 58° = 103°.

Задача 1 Внешний угол треугольника равен 115°, а один из несмежных внутренних углов равен 28°. Вычислите значения остальных углов треугольника.

Решение Для удобства используйте обозначения, приведенные на диаграмме выше. Пусть α — известный внутренний угол.

По теореме: β = γ — α = 115° — 28° = 87° .

Угол λ является смежным с внешними углами и вычисляется по следующей формуле (в соответствии со свойствами внешних углов): λ = 180° — γ = 180° — 115° = 65° ……..

Теоремы о внешних углах треугольника. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Сумма внешних углов

Сумма трех внешних углов треугольника, состоящего из разных вершин, равна 360°.

Рассмотрим треугольник ABC.

Каждая пара углов (внутренний угол и смежный с ним внешний угол) в сумме равна 180°. Сумма трех внутренних и трех внешних углов равна 540°.

(угол 1 + угол 4) + (угол 2 + угол 5) + (угол 3 + угол 6) = 180° + 180° + 180° = 540°

Это означает, что для нахождения суммы внешних углов необходимо из суммы внутренних углов вычесть сумму внутренних.

∠1 + ∠2 + ∠3 = 540° — (∠4 + ∠5 + ∠6) = 540° — 180° = 360°

Изучите видео ролик ниже:

видео YouTube

Давайте введем еще одно понятие — прямоугольные треугольники. Поскольку мы говорим о типах треугольников и углах, нам необходимо поговорить о правильных треугольниках.

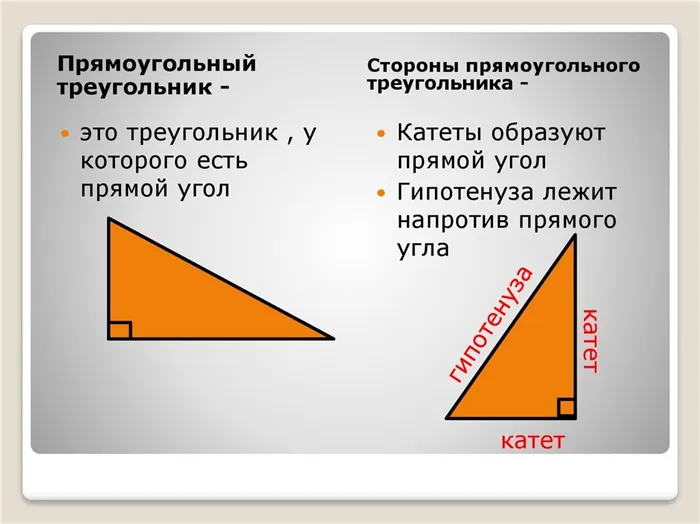
Заслуживающее внимания содержание. Если углы треугольника равны 180° и один из прямых треугольников имеет угол 90°, то два других из трех равны 180 — 90 = 90°. Это означает, что мы можем заключить, что два угла прямоугольного треугольника острые, а один — прямоугольный.

Сумма углов этих треугольников равна сумме всех внутренних углов n-угольника плюс сумма всех углов, вершина которых равна O. Таким образом, сумма всех углов n-угольника равна

Внешний угол

Внешние углы треугольника — это углы, примыкающие к внутренним углам. В треугольнике есть три внутренних угла, сумма которых равна 180 градусам. Смежные углы — это углы, у которых одна сторона лежит на одной прямой, а другая — общая.

Что необходимо для того, чтобы увидеть внешние углы треугольника? Это требует дополнительной работы. Чтобы увидеть внешние углы треугольника, необходимо продолжить его стороны. Каждая вершина имеет две стороны, поэтому если мы продолжим две прямые линии, то получим два смежных угла.

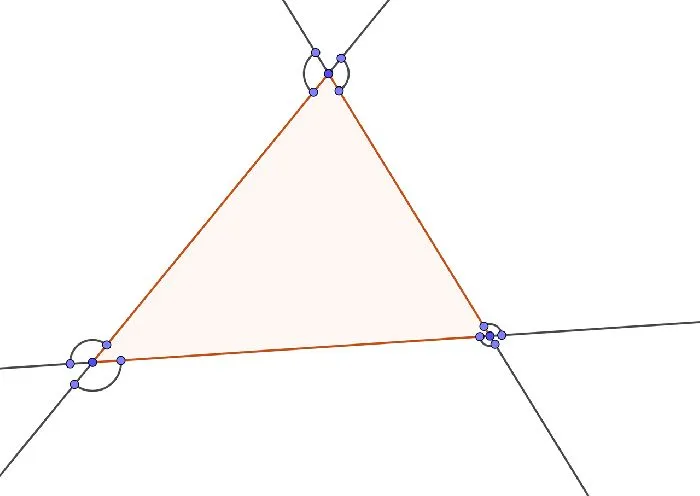
Рисунок 1: Внешние углы треугольника.

У треугольника всего шесть внешних углов.

Не рекомендуется рисовать на диаграмме два внешних угла при одной и той же вершине. Это усложняет конструкцию и часто ничего не дает.

Свойства внешних углов

Существует не так много свойств внешних углов треугольника, все они связаны с определением внешних углов.

Основное свойство: внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Это свойство доказывается довольно просто. Сумма смежных углов равна 180. Сумма углов треугольника равна все тем же 180. Тогда, если внутренние углы равны a, b, c, а внешние — d, то

Вычтите второе уравнение из первого, чтобы найти.

d=c+c — вот доказательство.

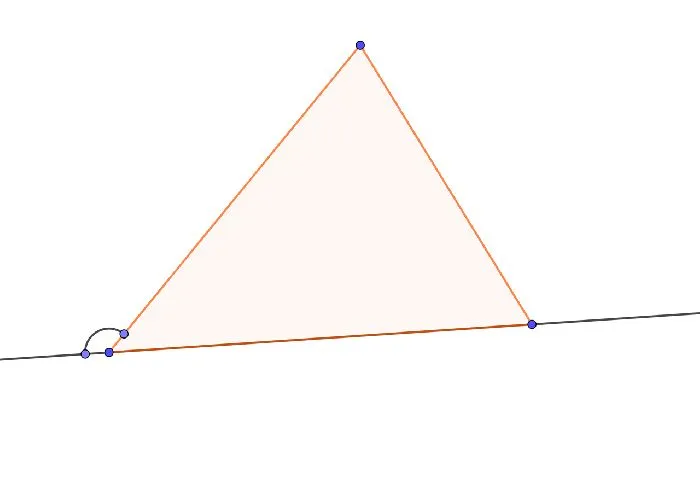
Рисунок 2: От диаграммы к доказательству

Существует еще несколько свойств внешних углов.

• Если для решения задачи требуется, чтобы два внешних угла существовали одновременно при одной и той же вершине на чертеже, то можно заметить, что эти внешние углы равны как вертикальные углы.
• Сумма трех внешних углов, по одному в каждой вершине, равна 360 градусам.
• Поскольку внешние и внутренние углы треугольника прилегают друг к другу, их сумма равна 180 градусам.

Именно внешние углы особенно важны при решении тупоугольных треугольников. Дело в том, что в тупоугольных треугольниках одна из высот всегда находится снаружи. Эта высота может быть найдена с помощью тригонометрических функций. Для этого необходимо знать угол. Треугольники с тупыми углами являются внешними углами, а завершенные прямоугольные треугольники — внутренними.

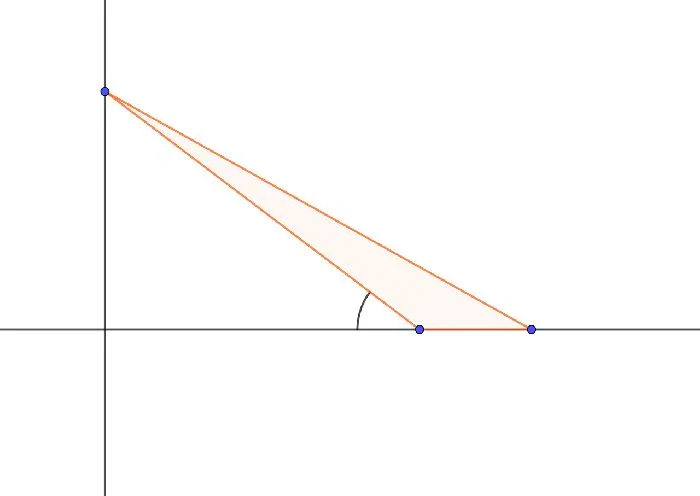
Рисунок 3: Внешние углы треугольника с тупыми углами.

Угол, прилежащий к внутреннему углу (λ) треугольника, является внешним углом при той же вершине. На диаграмме это обозначено γ.

Внешний угол

Внешние углы треугольника — это углы, примыкающие к внутренним углам. В треугольнике есть три внутренних угла, сумма которых равна 180 градусам. Последовательные углы — это углы, одна сторона которых лежит на прямой, а другая — общая.

Как можно увидеть внешние углы треугольника? Это требует дополнительной работы. Чтобы увидеть внешние углы треугольника, нужно расширить его стороны. Каждая вершина имеет две стороны, поэтому если мы продолжим две прямые линии, то получим два смежных угла.

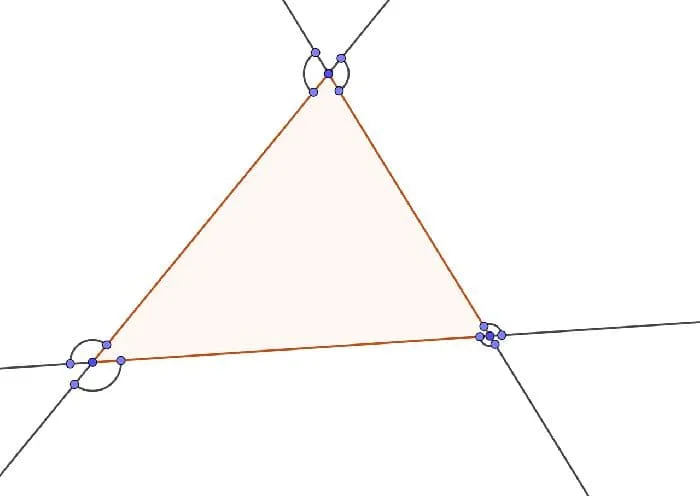
Рисунок 1: Внешние углы треугольника.

У треугольника всего шесть внешних углов.

Не рекомендуется рисовать на диаграмме два внешних угла при одной и той же вершине. Это усложняет конструкцию и часто ничего не дает.

Свойства внешних углов

Существует не так много свойств внешних углов треугольника, все они связаны с определением внешних углов.

Основное свойство: внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Это свойство доказывается довольно просто. Сумма смежных углов равна 180. Сумма углов треугольника равна все тем же 180. Тогда, если внутренние углы равны a, b, c, а внешние — d, то

Вычтите второе уравнение из первого, чтобы найти.

d=c+c — вот доказательство.

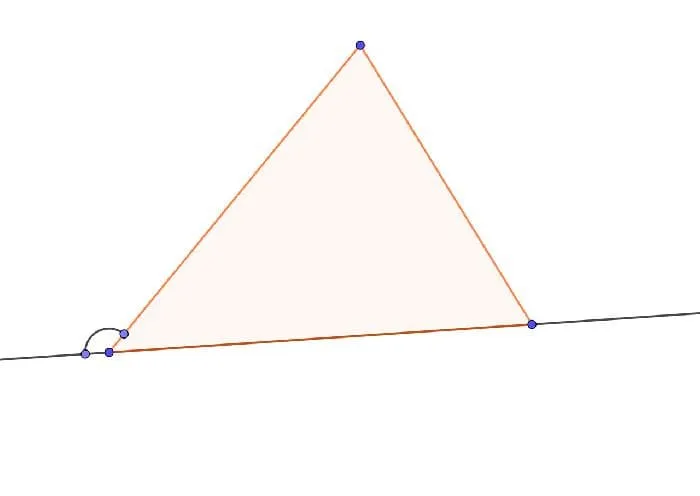
Рисунок 2: От диаграммы к доказательству

Существует еще несколько свойств внешних углов.

• Если для решения задачи требуется, чтобы два внешних угла существовали одновременно при одной и той же вершине на чертеже, то можно заметить, что эти внешние углы равны как вертикальные углы.
• Сумма трех внешних углов, по одному при каждой вершине, равна 360 градусам.
• Поскольку внешние и внутренние углы треугольника являются смежными, их сумма равна 180 градусам.

Именно внешние углы особенно важны при решении тупоугольных треугольников. Дело в том, что в тупоугольных треугольниках одна из высот всегда находится снаружи. Эта высота может быть найдена с помощью тригонометрических функций. Для этого необходимо знать угол. Треугольники с тупыми углами являются внешними углами, а завершенные прямоугольные треугольники — внутренними.

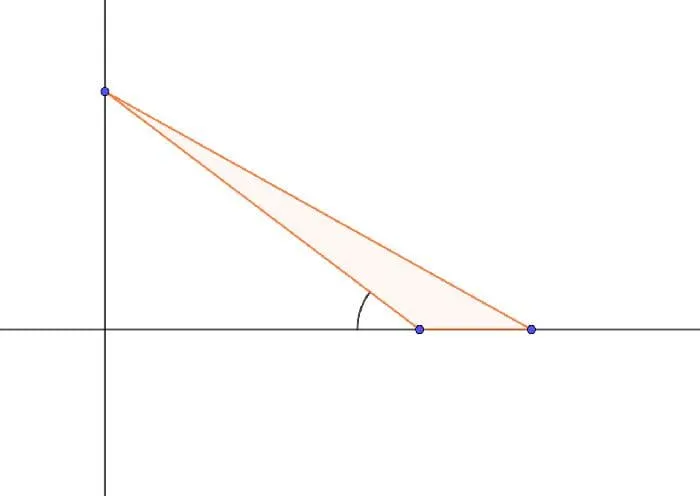
Рисунок 3: Внешние углы треугольника с тупыми углами.